题目内容
19.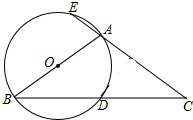 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,若AC=3AE,则tan∠ABC=$\frac{\sqrt{2}}{2}$.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,若AC=3AE,则tan∠ABC=$\frac{\sqrt{2}}{2}$.
分析 要求tan∠ABC的值,只要求除∠C的正切值即可,因为AB=AC,则∠ABC=∠C,要求∠C的正切值,则需要构造直角三角形,因而连接BE,由于AB是直径,则∠BEA=90°,然后根据题目中的条件可以求出BE、CE的长,从而可以得到∠C的正切值,本题得以解决.
解答 解:连接BE,如下图所示,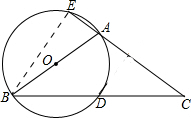
∵AB为⊙O的直径,
∴∠AEB=90°,
∵AC=3AE,AB=AC,
∴设AE=x,则AB=AC=3x,∠ABC=∠C,
∴$BE=\sqrt{A{B}^{2}-A{E}^{2}}=\sqrt{(3x)^{2}-{x}^{2}}=2\sqrt{2}x$,
∴tan∠C=$\frac{BE}{CE}=\frac{BE}{AE+AC}=\frac{2\sqrt{2}x}{x+3x}=\frac{\sqrt{2}}{2}$,
∴tan∠ABC=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查圆周角定理、等腰三角形的性质、解直角三角形,解题的关是明确题意,利用数形结合的数学思想,构造直角三角形,然后找出所求问题需要的条件进行解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.小华想找一个解是2的方程,那么他会选择( )
| A. | 3x+6=0 | B. | $\frac{2}{3}$x=2 | C. | 5-3x=1 | D. | 3(x-1)=x+1 |
8.一元二次方程x2-1=0的根是( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | ±1 |
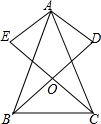 如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.
如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.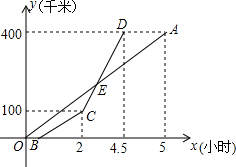 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题: