题目内容
7.先阅读第(1)题的解法,再解答第(2)题.(1)已知a、b是有理数,并且满足等式5-a$\sqrt{3}$=2b+$\frac{2}{3}\sqrt{3}$-a,求a、b的值.
解:因为5-a$\sqrt{3}$=2b+$\frac{2}{3}\sqrt{3}$.
即5-a$\sqrt{3}$=(2b-a)+$\frac{2}{3}\sqrt{3}$.
所以2b-a=5,-a=$\frac{2}{3}$.
解得:a=-$\frac{2}{3}$,b=$\frac{16}{3}$.
(2)设x、y是有理数,并且满足x2+$\sqrt{2}$y+2y=-4$\sqrt{2}$+17,求x+y的值.
分析 利用等式左右两边的有理数相等和二次根式相同,建立方程,然后解方程即可.
解答 解:因为x2+$\sqrt{2}$y+2y=-4$\sqrt{2}$+17,
所以(x2+2y)+$\sqrt{2}$y=17-4$\sqrt{2}$,
所以x2+2y=17,y=-4,
解得x=5,y=-4或x=-5,y=-4.
所以x+y=1或x+y=-9.
点评 此题是一个阅读题目,主要考查了实数的运算.对于阅读理解题要读懂阅读部分,然后依照同样的方法和思路解题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.下列式子中,是一元一次方程的是( )
| A. | x+1 | B. | x+1=2 | C. | x+y=1 | D. | x2+1=2 |
16.已知直角坐标系中,点P(x,y)满足(5x+2y-12)2+|3x+2y-6|=0,则点P坐标为( )
| A. | (3,-1.5) | B. | (-3,-1.5) | C. | (-2,-3) | D. | (2,-3) |
17. 如图的两个四边形相似,则∠α的度数是( )
如图的两个四边形相似,则∠α的度数是( )
 如图的两个四边形相似,则∠α的度数是( )
如图的两个四边形相似,则∠α的度数是( )| A. | 87° | B. | 60° | C. | 75° | D. | 120° |
 已知AD⊥BC,CE⊥AB,AB=BC.
已知AD⊥BC,CE⊥AB,AB=BC.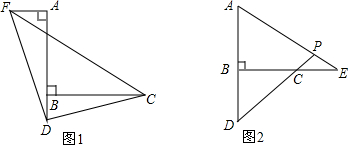
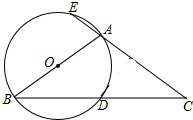 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,若AC=3AE,则tan∠ABC=$\frac{\sqrt{2}}{2}$.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,若AC=3AE,则tan∠ABC=$\frac{\sqrt{2}}{2}$.