题目内容
15.计算:(1)(x-2y)-3
(2)$\frac{x}{x-1}-\frac{1}{x+1}$.
分析 (1)首先转化为正整数指数次幂,然后利用乘方的性质求解;
(2)首先通分,然后进行减法运算即可.
解答 解:(1)原式=($\frac{y}{{x}^{2}}$)-3
=($\frac{{x}^{2}}{y}$)3
=$\frac{x^6}{y^3}$;
(2)原式=$\frac{x(x+1)}{(x-1)(x+1)}-\frac{x-1}{(x-1)(x+1)}$
=$\frac{{{x^2}+x-x+1}}{(x-1)(x+1)}$
=$\frac{{{x^2}+1}}{{{x^2}-1}}$.
点评 本题主要考查了零指数幂,负整数指数幂的运算.负整数指数为正整数指数的倒数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )


| A. | 只有乙 | B. | 只有丙 | C. | 甲和乙 | D. | 乙和丙 |
4.若x1,x2方程2x2-6x+3=0的两个实数根,则x1+x2+2x1•x2的值是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
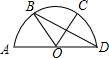 如图,AD为直径,∠A0B=∠BOC=∠COD.O为圆心,那么弧AB所对的圆心角是∠AOB;弧BD所对的圆心角是∠BOD;与弧AB相等的弧有$\widehat{BC}$、$\widehat{CD}$;BD与CO的位置关系是互相垂直平分.
如图,AD为直径,∠A0B=∠BOC=∠COD.O为圆心,那么弧AB所对的圆心角是∠AOB;弧BD所对的圆心角是∠BOD;与弧AB相等的弧有$\widehat{BC}$、$\widehat{CD}$;BD与CO的位置关系是互相垂直平分.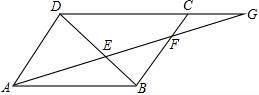 如图,?ABCD中,点G在DC的延长线上,AG分别交BD、BC于点E、F,图中△ABE∽△GDE,与△ADE相似的三角形有△FBE,与△CFG相似的三角形有△DAG,△BFA.
如图,?ABCD中,点G在DC的延长线上,AG分别交BD、BC于点E、F,图中△ABE∽△GDE,与△ADE相似的三角形有△FBE,与△CFG相似的三角形有△DAG,△BFA.