题目内容
3.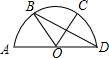 如图,AD为直径,∠A0B=∠BOC=∠COD.O为圆心,那么弧AB所对的圆心角是∠AOB;弧BD所对的圆心角是∠BOD;与弧AB相等的弧有$\widehat{BC}$、$\widehat{CD}$;BD与CO的位置关系是互相垂直平分.
如图,AD为直径,∠A0B=∠BOC=∠COD.O为圆心,那么弧AB所对的圆心角是∠AOB;弧BD所对的圆心角是∠BOD;与弧AB相等的弧有$\widehat{BC}$、$\widehat{CD}$;BD与CO的位置关系是互相垂直平分.
分析 根据圆心角、弧间的关系求得∠A0B=∠BOC=∠COD=60°,AB=BC=CD.进而求得∠BOD=120°,由等边三角形的性质得出OB=OD=CD=BC,从而证得四边形OBCD是菱形,根据菱形的性质即可证得BD与CO的位置关系.
解答 :如图,∵AD是⊙O的直径,∠A0B=∠BOC=∠COD,
∴$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,
∴∠A0B=∠BOC=∠COD=60°,AB=BC=CD.
∴∠BOD=120°,
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴AB=OA=OB=OD,
∴OB=OD=CD=BC,
∴四边形OBCD是菱形,
∴BD与CO互相垂直平分.
故答案分别是:∠AOB,∠BOD,$\widehat{BC}$、$\widehat{CD}$,互相垂直平分.
点评 本题考查了圆心角、弧、弦的关系.三者关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合.

练习册系列答案
相关题目
8.下列分子中,是最简分式的是( )
| A. | $\frac{x+y}{-x-y}$ | B. | $\frac{{a}^{2}+{b}^{2}}{a+b}$ | C. | $\frac{{a}^{2}-9}{a+3}$ | D. | $\frac{x+1}{{x}^{2}-x-2}$ |
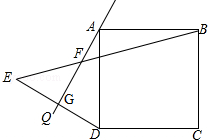 在小学,我们已经初步了解到,正方形的每个角都是90°,每条边都相等.如图,在正方形ABCD外侧作直线AQ,且∠QAD=30°,点D关于直线AQ的对称点为E,连接DE、BE,DE交AQ于点G,BE交AQ于点F.
在小学,我们已经初步了解到,正方形的每个角都是90°,每条边都相等.如图,在正方形ABCD外侧作直线AQ,且∠QAD=30°,点D关于直线AQ的对称点为E,连接DE、BE,DE交AQ于点G,BE交AQ于点F.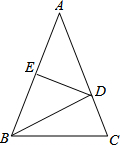 如图,△ABC中,AB=AC=10,线段AB的垂直平分线DE交边AB、AC分别于点E、D,
如图,△ABC中,AB=AC=10,线段AB的垂直平分线DE交边AB、AC分别于点E、D, 已知A(0,1)、B(3,1)、C(4,3),如果在y轴的左侧存在一点D,使得△ABD与△ABC全等,那么点D的坐标为(-1,3)或(-1,-1).
已知A(0,1)、B(3,1)、C(4,3),如果在y轴的左侧存在一点D,使得△ABD与△ABC全等,那么点D的坐标为(-1,3)或(-1,-1).