题目内容
 如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.
如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.(1)求证:△ADE≌△CBF.
(2)请你添加一个条件:
考点:菱形的判定,全等三角形的判定与性质,平行四边形的性质
专题:
分析:(1)根据平行四边形的对边相等的性质可以得到AD=BC,AB=CD,又点E、F是AB、CD中点,所以AE=CF,然后利用边角边即可证明两三角形全等;
(2)连接EF,可以证明四边形AEFD是平行四边形,所以AD∥EF,又AD⊥BD,所以BD⊥EF,根据菱形的判定可以得到四边形是菱形.
(2)连接EF,可以证明四边形AEFD是平行四边形,所以AD∥EF,又AD⊥BD,所以BD⊥EF,根据菱形的判定可以得到四边形是菱形.
解答: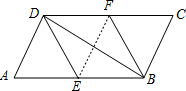 证明:(1)在?ABCD中,AD=BC,AB=CD,∠A=∠C,
证明:(1)在?ABCD中,AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=CF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)添加AD⊥BD.
理由如下:连接EF,在?ABCD中,E、F分别为边AB、CD的中点,
∴DF平行且等于AE,
∴四边形AEFD是平行四边形,
∴EF∥AD,
∵AD⊥BD,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形.
 证明:(1)在?ABCD中,AD=BC,AB=CD,∠A=∠C,
证明:(1)在?ABCD中,AD=BC,AB=CD,∠A=∠C,∵E、F分别为边AB、CD的中点,
∴AE=CF,
在△ADE和△CBF中,
|
∴△ADE≌△CBF(SAS);
(2)添加AD⊥BD.
理由如下:连接EF,在?ABCD中,E、F分别为边AB、CD的中点,
∴DF平行且等于AE,
∴四边形AEFD是平行四边形,
∴EF∥AD,
∵AD⊥BD,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形.
点评:本题主要考查了平行四边形的性质,全等三角形的判定以及菱形的判定,利用好E、F是中点是解题的关键.

练习册系列答案
相关题目

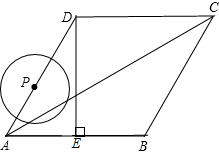 如图,在菱形ABCD中,∠BAD=60°,DE⊥AB于点E,且AE=2,动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.
如图,在菱形ABCD中,∠BAD=60°,DE⊥AB于点E,且AE=2,动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.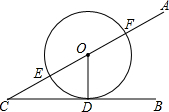 如图,∠ACB=30°,D为CB上一点,CD=
如图,∠ACB=30°,D为CB上一点,CD=