题目内容
4．在△ABC中，AB=AC，一条直线恰好将△ABC分成两个等腰三角形，那么∠ABC的度数可能是45°或36°或72°或（$\frac{540}{7}$）°．分析 因为题中没有指明是过顶角的顶角的顶点还是过底角的顶点，故应该分四情况进行分析，从而求解．
解答 解：①如图①，∠CAB=90°AB=AC，
则∠ABC=45°；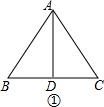
②AB=AC，则∠ABC=36°；
③AB=AC，AD=BD，BD=BC，则∠ABC=72°；
④AB=AC，AD=BD，CD=BC，∠ABC=$\frac{540}{7}$°；
故答案为：45°或36°或72°或（$\frac{540}{7}$）°．
点评 本题考查了等腰三角形的性质，解题的关键是能够正确的分类讨论，难度较大．
练习册系列答案
相关题目
如图，DE是△ABC的中位线，延长DE到F，使EF=DE，连接BF
的对称轴是直线（ ）
的顶点都是正方形网格中的格点，则 
等于( ) 
B. 
C. 
D. 
B. 
C. 
D. 
16．
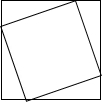一个周长为20的正方形内接于一个周长为28的正方形，那么从里面正方形的顶点到外面正方形的顶点的最大距离是（ ）
一个周长为20的正方形内接于一个周长为28的正方形，那么从里面正方形的顶点到外面正方形的顶点的最大距离是（ ）| A． | $\sqrt{58}$ | B． | $\frac{7}{2}$$\sqrt{5}$ | C． | 8 | D． | $\sqrt{65}$ | ||||
| E． | 5$\sqrt{3}$ |