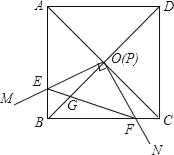
题目内容
【题目】如图,![]() 的半径为
的半径为![]() ,点
,点![]() 、
、![]() 、
、![]() 、
、![]() 在
在![]() 上,且四边形
上,且四边形![]() 是矩形,点
是矩形,点![]() 是劣弧
是劣弧![]() 上一动点,
上一动点,![]() 、
、![]() 分别与
分别与![]() 相交于点
相交于点![]() 、点
、点![]() .当
.当![]() 且
且![]() 时,
时,![]() 的长度为( )
的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
作辅助线,构建矩形的对角线,根据等边对等角得∠ABP=∠APB,由同弧所对的圆周角相等可得∠ACB=∠ACP,进而得到AF=FC.根据矩形的四个角都是直角得∠ABC=90°,AE=EF=FD得FC=2FD,∠DCF=30°,得出∠ACB=30°,求出BC的长,AD的长,再三等分即可.
连接AC、BD.
∵PA=AB,∴∠ABP=∠APB.
∵∠ABP=∠ACP,∠APB=∠ACB,∴∠ACB=∠ACP.
∵AD∥BC,∴∠DAC=∠ACB,∴∠ACP=∠DAC,∴AF=FC.
∵AE=EF=FD,设FD=x,则FC=AF=2x.
∵四边形ABCD为矩形,∴AD=BC,∠ABC=∠ADC=90°,∴AC为⊙O的直径.
在Rt△DFC中,FC=2FD,∴∠DCF=30°,∴∠ACB=∠ACP=30°.
∵⊙O的半径为1,∴AC=2,∴AB=1,BC=![]() ,∴AD=BC=
,∴AD=BC=![]() .
.
∵AE=EF=FD,∴AE=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程. 在画函数图象时,我们通过描点、平移、对称的方法画出了所学的函数图象. 同时,我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题
,结合上面经历的学习过程,现在来解决下面的问题
在函数![]() 中,自变量
中,自变量![]() 的取值范围是全体实数,下表是
的取值范围是全体实数,下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
|
| 0 | 1 | 2 | 3 | ||
y | … | 0 | 1 | 2 | 3 | 2 | … |
(1)根据表格填写:![]() _______.
_______.
(2)化简函数解析式:
当![]() 时,
时,![]() _______;
_______;
当![]() 时,
时,![]() ______.
______.
(3)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并解决以下问题;
①该函数的最大值为_______.
②若![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ________.
________.
③根据图象可得关于![]() 的方程
的方程![]() 的解为_______.
的解为_______.
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,连结
上一动点,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对![]() 的面积与
的面积与![]() 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:

(1)设![]() 的长度为
的长度为![]() ,
,![]() 的面积
的面积![]() ,通过取
,通过取![]() 边上的不同位置的点
边上的不同位置的点![]() ,经分析和计算,得到了
,经分析和计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根据上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐标系![]() 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.

(3)在(1)的条件下,令![]() 的面积为
的面积为![]() .
.
①用![]() 的代数式表示
的代数式表示![]() .
.
②结合函数图象.解决问题:当![]() 时,
时,![]() 的取值范围为______.
的取值范围为______.