��Ŀ����
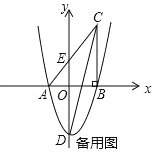
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ���е㣬
���е㣬![]() �DZ�
�DZ�![]() ��һ���㣬����
��һ���㣬����![]() ��ȡ
��ȡ![]() ���е�
���е�![]() ������
������![]() .С�θ���ѧϰ�����ľ��飬��
.С�θ���ѧϰ�����ľ��飬��![]() �������
�������![]() �ij���֮��Ĺ�ϵ������̽����
�ij���֮��Ĺ�ϵ������̽����

��1����![]() �ij���Ϊ
�ij���Ϊ![]() ��
��![]() �����
�����![]() ��ͨ��ȡ
��ͨ��ȡ![]() ���ϵIJ�ͬλ�õĵ�
���ϵIJ�ͬλ�õĵ�![]() ���������ͼ��㣬�õ���
���������ͼ��㣬�õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
�����ϱ���֪��![]() ______��
______��![]() ______.
______.
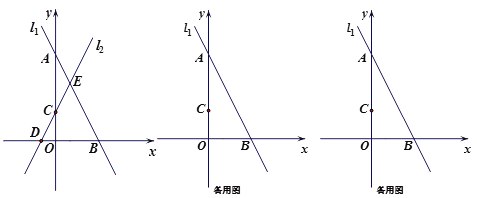
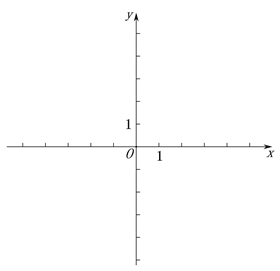
��2����ƽ��ֱ������ϵ![]() �У�������1������ȷ���ĺ�����ͼ��.
�У�������1������ȷ���ĺ�����ͼ��.

��3���ڣ�1���������£���![]() �����Ϊ
�����Ϊ![]() .
.
����![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() .
.
�ڽ�Ϻ���ͼ��.������⣺��![]() ʱ��
ʱ��![]() ��ȡֵ��ΧΪ______.
��ȡֵ��ΧΪ______.
���𰸡���1��![]() ��
��![]() .��2������������3����
.��2������������3����![]() ����
����![]()
��������
��1����ͨ�����е���֪���ݵó�![]() �ĸߣ�Ȼ���ٴ��뵽�����ʽ�м��ɵó��𰸣�
�ĸߣ�Ȼ���ٴ��뵽�����ʽ�м��ɵó��𰸣�
��2�����ݱ��е�������㣬�����ɣ�
��3����ֱ�����������ʽ�����ߵ����ʼ��ɵó��𰸣�
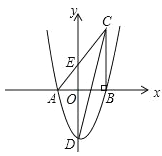
�ڽ�����ͼ����ͬһ��ֱ������ϵ�У���ͼ���м��ɵó���.
��1����![]() ��DE���ϵĸ�Ϊh
��DE���ϵĸ�Ϊh
��![]() ʱ��
ʱ��![]() ��֪
��֪![]()
��![]() ʱ��
ʱ��![]() ����
����![]()
�൱![]() ʱ��
ʱ��![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]()
��2��
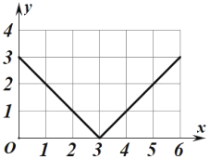
��3����������ɵ���![]() ����
����![]() �ϵĸ�Ϊ2.
�ϵĸ�Ϊ2.
��![]() .
.
��F��AE���е�
��![]() .
.
����ͼ
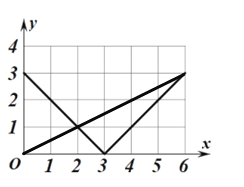
����ͼ���֪��![]() ʱ��
ʱ��![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]()

��ϰ��ϵ�д�
�����Ŀ