Question

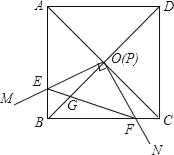
【题目】如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G．

（1）求四边形OEBF的面积；

（2）求证：OGBD=EF2；

（3）在旋转过程中，当△BEF与△COF的面积之和最大时，求AE的长．

Answer 1

【答案】（1）；（2）详见解析；（3）AE=．

【解析】

（1）由四边形ABCD是正方形，直角∠MPN，易证得△BOE≌△COF（ASA），则可证得S四边形OEBF=S△BOC=S正方形ABCD；

（2）易证得△OEG∽△OBE，然后由相似三角形的对应边成比例，证得OGOB=OE2，再利用OB与BD的关系，OE与EF的关系，即可证得结论；

（3）首先设AE=x，则BE=CF=1﹣x，BF=x，继而表示出△BEF与△COF的面积之和，然后利用二次函数的最值问题，求得AE的长．

（1）∵四边形ABCD是正方形，

∴OB=OC，∠OBE=∠OCF=45°，∠BOC=90°，

∴∠BOF+∠COF=90°，

∵∠EOF=90°，

∴∠BOF+∠COE=90°，

∴∠BOE=∠COF，

在△BOE和△COF中，

∴△BOE≌△COF（ASA），

∴S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=S正方形ABCD

（2）证明：∵∠EOG=∠BOE，∠OEG=∠OBE=45°，

∴△OEG∽△OBE，

∴OE：OB=OG：OE，

∴OGOB=OE2，

∵

∴OGBD=EF2；

（3）如图，过点O作OH⊥BC，

∵BC=1，

∴

设AE=x，则BE=CF=1﹣x，BF=x，

∴S△BEF+S△COF=BEBF+CFOH

∵

∴当时，S△BEF+S△COF最大；

即在旋转过程中，当△BEF与△COF的面积之和最大时，