题目内容
13.三张完全相同的卡片,正面分别标有数字0,1,2,先将三张卡片洗匀后反面朝上,随机抽取一张,记下卡片上的数字m,放置一边,再从剩余的卡片中随机抽取一张卡片,记下卡片上的数字n,则满足关于x的方程x2+mx+n=0有实数根的概率为$\frac{1}{2}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与满足关于x的方程x2+mx+n=0有实数根的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,满足关于x的方程x2+mx+n=0有实数根的有3种情况,
∴满足关于x的方程x2+mx+n=0有实数根的概率为:$\frac{3}{6}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率以及根的判别式.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,CD⊥AB,求证:△ACD∽△ABC∽△CBD.
如图,在△ABC中,∠ACB=90°,CD⊥AB,求证:△ACD∽△ABC∽△CBD.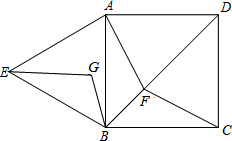 已知正方形ABCD中,F为对角线BD(不含B点)上任意一点,△ABE为正三角形,若BF=BG且∠FBG=60°,连接EG、AF、CF.
已知正方形ABCD中,F为对角线BD(不含B点)上任意一点,△ABE为正三角形,若BF=BG且∠FBG=60°,连接EG、AF、CF.
 如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E,若DE=1,∠C=30°,则图中阴影部分的面积是$\frac{4}{9}$π-$\frac{\sqrt{3}}{3}$.
如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E,若DE=1,∠C=30°,则图中阴影部分的面积是$\frac{4}{9}$π-$\frac{\sqrt{3}}{3}$.