题目内容
1.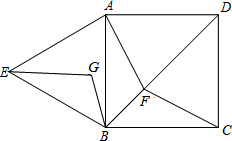 已知正方形ABCD中,F为对角线BD(不含B点)上任意一点,△ABE为正三角形,若BF=BG且∠FBG=60°,连接EG、AF、CF.
已知正方形ABCD中,F为对角线BD(不含B点)上任意一点,△ABE为正三角形,若BF=BG且∠FBG=60°,连接EG、AF、CF.(1)求证:EG=CF;
(2)当F点在何处时,AF+CF的值最小,并说明理由;
(3)当F点在何处时,AF+CF+BF的值最小,并说明理由;
(4)AF+CF+BF的值最小为$\sqrt{3}+1$时,求正方形的边长.
分析 (1)根据正方形的性质得到∠ABF=∠CBF=45°,AB=BC,由△ABE是等边三角形,得到AB=BE,∠ABE=60°,等量代换得到BE=BC,∠EBG=∠CBF,根据全等三角形的判定定理即可得到结论;
(2)根据两点之间线段最短,即可得到A,F,C三点共线时,AF+CF的值最小.
(3)连接CE,当F点位于BD与CE的交点处时,AF+CF+BF的值最小,通过全等三角形得到AF=EG,由已知条件得到△BGF是等边三角形.求出BF=GF.推出AF+BF+CF=EG+GF+CF.根据“两点之间线段最短得到EG+GF+CF=EC最短;于是得到结论;
(4)过E点作EM⊥BC交CB的延长线于M,由题意求出∠EBM=30°,设正方形的边长为x,在Rt△EMC中,根据勾股定理求得正方形的边长为$\sqrt{2}$.
解答 解:(1)∵四边形ABCD是正方形,
∴∠ABF=∠CBF=45°,AB=BC,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∵∠GBF=60°,
∴∠EBG=∠ABF,∴BE=BC,∠EBG=∠CBF,
在△BEG与△CBF中,$\left\{\begin{array}{l}{BE=BC}\\{∠EBG=∠CBF}\\{BG=BF}\end{array}\right.$,
∴△EBG≌△CBF,∴EG=CF;
(2)当F点落在BD的中点时,A,F,C三点共线,由两点之间,线段最短得AF+CF的值最小;
(3)如图1,连接CE,当F点位于BD与CE的交点处时,AF+CF+BF的值最小,
理由如下:连接FG,在△AFB与△EGB中,$\left\{\begin{array}{l}{AB=BE}\\{∠ABF=∠EBG}\\{BF=BG}\end{array}\right.$,
∴△ABF≌△EBG,
∴AF=EG,
∵∠GBF=60°,GB=FB,
∴△BBGF是等边三角形.
∴BF=GF.
∴AF+BF+CF=EG+GF+CF.
根据“两点之间线段最短”,得EG+GF+CF=EC最短;
∴当F点位于BD与CE的交点处时,AF+BF+CF的值最小,即等于EC的长;
(4)解:过E点作EM⊥BC交CB的延长线于M,
∴∠EBM=90°-60°=30°,
设正方形的边长为x,则BM=$\frac{\sqrt{3}}{2}$x,EM=$\frac{x}{2}$,
在Rt△EMC中,
∵EM2+MC2=EC2,
∴($\frac{x}{2}$)2+($\frac{\sqrt{3}}{2}$x+x)2=($\sqrt{3}$+1)2.
解得,x=$\sqrt{2}$(舍去负值).
∴正方形的边长为$\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,正方形的性质,等边三角形的性质和判定,勾股定理,熟练掌握两点之间线段最短是解题的关键.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 91 | B. | 98 | C. | 78 | D. | 116 |
 如图,在△ABC中,DE∥BC,若BF:EF=3:2,求$\frac{AD}{AB}$和$\frac{EA}{EC}$的值.
如图,在△ABC中,DE∥BC,若BF:EF=3:2,求$\frac{AD}{AB}$和$\frac{EA}{EC}$的值.
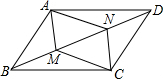 如图,平行四边形ABCD中,M,N为对角线BD上不同的两点,且BM=DN,连接AM、MC、CN、AN.求证:四边形AMCN是平行四边形.
如图,平行四边形ABCD中,M,N为对角线BD上不同的两点,且BM=DN,连接AM、MC、CN、AN.求证:四边形AMCN是平行四边形.