题目内容
4．
如图，在△ABC中，∠ACB=90°，CD⊥AB，求证：△ACD∽△ABC∽△CBD．
分析 利用等角的余角相等可得到∠ACD=∠B，则根据有两组角对应相等的两个三角形相似可判定△ACD∽△CBD，再利用∠DAC=∠CAB可判定△ACD∽△ABC，于是得到△ACD∽△ABC∽△CBD．
解答 解：∵CD⊥AB，
∴∠ADC=∠BDC=90°，
∵∠A+∠ACD=90°，∠A+∠B=90°，
∴∠ACD=∠B，
∵∠ADC=∠CDB，
∴△ACD∽△CBD，
∵∠DAC=∠CAB，
∵∠ADC=∠ACB，
∴△ACD∽△ABC，
∴△ACD∽△ABC∽△CBD．
点评 本题考查了相似三角形的判定：有两组角对应相等的两个三角形相似．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知关于x的一次函数y=kx+4的图象经过点（1，2）．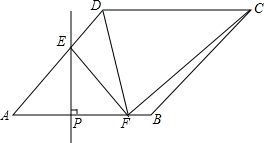
如图，在菱形ABCD中，∠DAB=45°，AB=4，点P为线段AB上一个动点，过点P作PE⊥AB交直线AD于点E，沿PE将∠A折叠，点A的对称点为点F，连接EF、DF、GF，当△CDF为直角三角形时，AP=$\sqrt{2}$或2+$\sqrt{2}$．．