题目内容
△ABC中,∠BAC=45°,S△ABC=12,BC=4,点D、E、F为BC、AB、AC边上的动点,则△DEF周长的最小值为 .
考点:轴对称-最短路线问题
专题:
分析:在BC上任取一点D,连接AD,把△ABD沿AB翻折得△ABD′,把△ACD沿AC翻折得△ACD″,连接D′D″交AB、AC于E、F.连接DE,DF,根据已知条件得出△AD′D″是等腰直角三角形,求得D′D″=
AD,此时△DEF周长的最小值=
AD,根据垂线段最短可知AD⊥BC时AD的值最小,由三角形的面积就可求得AD的最小值,从而求得△DEF的周长的最小值.
| 2 |
| 2 |
解答: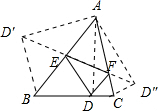 解:在BC上任取一点D,连接AD,
解:在BC上任取一点D,连接AD,
把△ABD沿AB翻折得△ABD′,把△ACD沿AC翻折得△ACD″,
∵∠BAC=45°,
∴∠D′AD″=90°,AD=AD′=AD″,
连接D′D″交AB、AC于E、F.连接DE,DF,
∵DE=D′E,DF=D″F,
∴△DEF的周长的最小值=DE+DF+EF=D′E+EF+D″F=D′D″=
AD,
∵根据垂线段最短可知AD⊥BC时AD的值最小,
∵S△ABC=12,BC=4,
∴AD的最小值=6,
∴△DEF的周长的最小值=6
.
故答案为:6
.
 解:在BC上任取一点D,连接AD,
解:在BC上任取一点D,连接AD,把△ABD沿AB翻折得△ABD′,把△ACD沿AC翻折得△ACD″,
∵∠BAC=45°,
∴∠D′AD″=90°,AD=AD′=AD″,
连接D′D″交AB、AC于E、F.连接DE,DF,
∵DE=D′E,DF=D″F,
∴△DEF的周长的最小值=DE+DF+EF=D′E+EF+D″F=D′D″=
| 2 |
∵根据垂线段最短可知AD⊥BC时AD的值最小,
∵S△ABC=12,BC=4,
∴AD的最小值=6,
∴△DEF的周长的最小值=6
| 2 |
故答案为:6
| 2 |
点评:本题考查了轴对称的性质,等腰直角三角形的性质,最短路线问题,作出D、E、F点是本题的关键.

练习册系列答案
相关题目
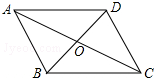 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )| A、17 | B、27 | C、34 | D、44 |
已知代数式x3-2x2+ax+6,当x=-1时,它的值是0,则a的值是( )
| A、7 | B、3 | C、0 | D、-3 |
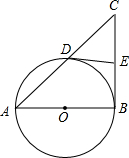 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E是BC的中点.求证:DE是⊙O的切线.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E是BC的中点.求证:DE是⊙O的切线.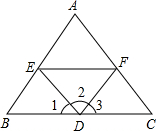 如图,请完成下列各题:
如图,请完成下列各题: