题目内容
7. 如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,tanC=$\frac{1}{2}$,求EF的长.
分析 (1)连接圆心和切点,利用平行,OF⊥CB可证得∠ODF=90°;
(2)过D作DH⊥BC于H,设BD=k,CD=2k,求得BD=2$\sqrt{5}$,CD=4$\sqrt{5}$,根据三角形的面积公式得到DH=$\frac{CD•BD}{BC}$=4,由勾股定理得到OH=$\sqrt{O{D}^{2}-D{H}^{2}}$=3,根据射影定理得到OD2=OH•OE,求得OE=$\frac{25}{3}$,得到BE=$\frac{10}{3}$,根据相似三角形的性质得到BF=2,根据勾股定理即可得到结论.
解答 (1)证明:如图,连接OD,BD,
∵AB是⊙O的直径,
∴∠ADB=∠90°,
∴BD⊥AC.
∵AB=BC,
∴AD=DC.
∵OA=OB,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD.
∴直线DE是⊙O的切线.
(2)过D作DH⊥BC于H,
∵⊙O的半径R=5,tanC=$\frac{1}{2}$,
∴BC=10,
设BD=k,CD=2k,
∴BC=$\sqrt{5}$k=10,
∴k=2$\sqrt{5}$,
∴BD=2$\sqrt{5}$,CD=4$\sqrt{5}$,
∴DH=$\frac{CD•BD}{BC}$=4,
∴OH=$\sqrt{O{D}^{2}-D{H}^{2}}$=3,
∵DE⊥OD,DH⊥OE,
∴OD2=OH•OE,
∴OE=$\frac{25}{3}$,
∴BE=$\frac{10}{3}$,
∵DE⊥AB,
∴BF∥OD,
∴△BFE∽△ODE,
∴$\frac{BF}{OD}=\frac{BE}{OE}$,即$\frac{BF}{5}=\frac{\frac{10}{3}}{\frac{25}{3}}$,
∴BF=2,
∴EF=$\sqrt{B{E}^{2}-B{F}^{2}}$=$\frac{8}{3}$.
点评 本题考查了直线与圆的位置关系,等腰直角三角形的性质以及解直角三角形.当题中已有垂直时,证直线为圆的切线,通常选用平行来进行证明;而求相关角的余弦值,应根据所给条件进行适当转移,注意利用直角三角形面积的不同方式求解.

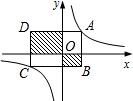 如图,在平面直角坐标系中,面积为a的矩形ABCD的边与坐标轴平行或垂直,顶点A、C分别在函数y=$\frac{1}{x}$的图象的两个分支上,则图中两块阴影部分面积的和等于a-2.(用含a的式子表示)
如图,在平面直角坐标系中,面积为a的矩形ABCD的边与坐标轴平行或垂直,顶点A、C分别在函数y=$\frac{1}{x}$的图象的两个分支上,则图中两块阴影部分面积的和等于a-2.(用含a的式子表示)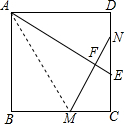 如图,正方形ABCD中,AB=2,E是CD中点,将正方形ABCD沿AM折叠,使点B的对应点F落在AE上,延长MF交CD于点N,则DN的长为2$\sqrt{5}$-4.
如图,正方形ABCD中,AB=2,E是CD中点,将正方形ABCD沿AM折叠,使点B的对应点F落在AE上,延长MF交CD于点N,则DN的长为2$\sqrt{5}$-4. 如图,将△ABC水平向右平移了acm后,得到△A'B'C',已知BC=6cm,B C'=17cm,那么a=11cm.
如图,将△ABC水平向右平移了acm后,得到△A'B'C',已知BC=6cm,B C'=17cm,那么a=11cm.