题目内容
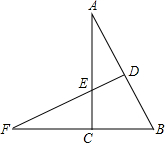 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,ED所在直线是线段AB的垂直平分线,若直线ED分别交AB、AC及BC的延长线于点D、E、F,连接BE,求证:EF=2DE.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,ED所在直线是线段AB的垂直平分线,若直线ED分别交AB、AC及BC的延长线于点D、E、F,连接BE,求证:EF=2DE.考点:线段垂直平分线的性质,含30度角的直角三角形
专题:证明题
分析:求出∠ABC=60°,根据线段的垂直平分线的性质得出∠EDA=90°,AE=BE,求出∠AED=60°,∠ABE=∠A=30°,求出∠EBC=∠ABE,根据角平分线性质求出EC=DE,求出EF=2CE,即可得出答案.
解答:证明:∵∠A=30°,∠ACB=90°,
∴∠ABC=60°,
∵ED所在直线是线段AB的垂直平分线,
∴∠EDA=90°,AE=BE,
∵∠A=30°,
∴∠AED=60°,∠ABE=∠A=30°,
∴∠EBC=30°=∠ABE,
∵∠ACB=90°,ED⊥AB,
∴CE=DE,
∵∠ACB=90°,
∴∠ECF=90°,
∵∠FEC=∠AED=60°,
∴∠F=30°,
∴EF=2CE,
∵EC=DE,
∴EF=2DE.
∴∠ABC=60°,
∵ED所在直线是线段AB的垂直平分线,
∴∠EDA=90°,AE=BE,
∵∠A=30°,
∴∠AED=60°,∠ABE=∠A=30°,
∴∠EBC=30°=∠ABE,
∵∠ACB=90°,ED⊥AB,
∴CE=DE,
∵∠ACB=90°,
∴∠ECF=90°,
∵∠FEC=∠AED=60°,
∴∠F=30°,
∴EF=2CE,
∵EC=DE,
∴EF=2DE.
点评:本题考查了线段垂直平分线性质,角平分线性质,三角形内角和定理,含30度角的直角三角形性质,三角形的内角和定理的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
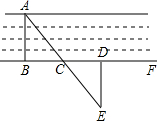 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )