题目内容
8.已知平行于x轴的直线y=m(m≠0)与函数y=x和函数y=$\frac{1}{x}$的图象分别交于点A和点B,在过A,B两点且顶点在直线y=x上的抛物线中,若线段AB=$\frac{3}{2}$,试求出满足条件的抛物线的解析式.分析 根据题意设$A(m,m),B(\frac{1}{m},m)$,根据$AB=|{m-\frac{1}{m}}|=\frac{3}{2}$,求得${m_1}=-\frac{1}{2}$,m2=2,m3=-2,m4=$\frac{1}{2}$,从而求得A(-$\frac{1}{2}$,-$\frac{1}{2}$),B(-2,-$\frac{1}{2}$)或A(2,2),B($\frac{1}{2}$,2),根据顶点在直线y=x上的抛物线中,得出顶点坐标为为$(-\frac{5}{4},-\frac{5}{4})$,$(\frac{5}{4},\frac{5}{4})$,利用待定系数法即可求得解析式.
解答 解:由题得$A(m,m),B(\frac{1}{m},m)$,
∴$AB=|{m-\frac{1}{m}}|=\frac{3}{2}$,
当m-$\frac{1}{m}$=$\frac{3}{2}$时,
解得${m_1}=-\frac{1}{2}$,m2=2,
∴A(-$\frac{1}{2}$,-$\frac{1}{2}$),B(-2,-$\frac{1}{2}$)或A(2,2),B($\frac{1}{2}$,2),
当m-$\frac{1}{m}$=-$\frac{3}{2}$时,
解得m3=-2,m4=$\frac{1}{2}$;
∴A(-2,-2),B(-$\frac{1}{2}$,-2)或A($\frac{1}{2}$,$\frac{1}{2}$),B(2,$\frac{1}{2}$),
当A(-2,-2),B(-$\frac{1}{2}$,-2)时,
顶点的横坐标为=$\frac{-2-\frac{1}{2}}{2}$=-$\frac{5}{4}$,
∵顶点在直线y=x上,
∴抛物线的顶点坐标为$(-\frac{5}{4},-\frac{5}{4})$;
A($\frac{1}{2}$,$\frac{1}{2}$),B(2,$\frac{1}{2}$),
同理:求得抛物线的顶点坐标为$(\frac{5}{4},\frac{5}{4})$;
∴抛物线的解析式为$y=±\frac{4}{3}{(x+\frac{5}{4})^2}-\frac{5}{4}$或$y=±\frac{4}{3}{(x-\frac{5}{4})^2}+\frac{5}{4}$.
点评 本题考查了待定系数法求二次函数的解析式,根据题意列出等式,求得顶点坐标是本题的关键.

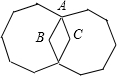 如图,平面上有两个全等的正八边形,∠BAC为( )
如图,平面上有两个全等的正八边形,∠BAC为( )| A. | 60° | B. | 45° | C. | 30° | D. | 72° |
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 1-3 |
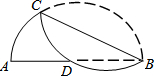 将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )
将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )| A. | 6$\sqrt{7}$ | B. | 16 | C. | 2$\sqrt{65}$ | D. | 4$\sqrt{15}$ |

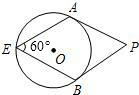 如图,点E是半径为6的⊙O上一点,过点E作一只60°的圆周角∠AEB,分别过点A、B作⊙O的切线,两条切线交于点P.那么四边形AEBP的面积的最大值是54$\sqrt{3}$.
如图,点E是半径为6的⊙O上一点,过点E作一只60°的圆周角∠AEB,分别过点A、B作⊙O的切线,两条切线交于点P.那么四边形AEBP的面积的最大值是54$\sqrt{3}$.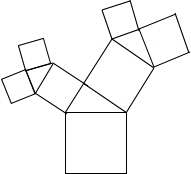 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2.
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2.