题目内容
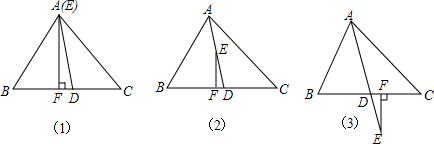
在△ABC中(∠B>∠C),AD平分∠BAC,E是AD上的一动点,过点E作EF⊥BC于点F.
(1)当点E与点A重合时,如图(1),若∠B=65°,∠C=45°,求∠DEF的度数;
(2)∠B、∠C、∠DE(A)F之间有何关系?请探讨,并证明你的结论;
(3)点E沿AD运动,当点E在AD内或点E在AD的延长线上时(E与点A、D不重合),见图(2)与图(3),∠B、∠C、∠DEF之间还有类似的规律吗?选择其中一种情况证明.
(1)当点E与点A重合时,如图(1),若∠B=65°,∠C=45°,求∠DEF的度数;
(2)∠B、∠C、∠DE(A)F之间有何关系?请探讨,并证明你的结论;
(3)点E沿AD运动,当点E在AD内或点E在AD的延长线上时(E与点A、D不重合),见图(2)与图(3),∠B、∠C、∠DEF之间还有类似的规律吗?选择其中一种情况证明.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据直角三角形的性质,可得∠DEF=90°-∠C-
∠BAC,根据三角形的内角和定理,可得90°-∠C-
∠BAC=90°-∠C-
(180°-∠B-∠C),根据去括号,可得答案;
(2)根据直角三角形的性质,可得∠DEF=90°-∠C-
∠BAC,根据三角形的内角和定理,可得90°-∠C-
∠BAC=90°-∠C-
(180°-∠B-∠C),根据去括号,可得答案;
(3)根据直角三角形的性质,可得∠DEF=90°-∠ADF,根据三角形的内角和定理,可得90°-∠ADF=90°-∠C-
∠BAC,根据去括号化简,可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据直角三角形的性质,可得∠DEF=90°-∠C-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据直角三角形的性质,可得∠DEF=90°-∠ADF,根据三角形的内角和定理,可得90°-∠ADF=90°-∠C-
| 1 |
| 2 |
解答:解:(1)当点E与点A重合时,
∠DEF=90°-∠C-
∠BAC
=90°-∠C-
(180°-∠B-∠C)
=
(∠B-∠C)
=
(65°-45°)
=10°;
(2)∠DEF=
(∠B-∠C)
当点E与点A重合时,
∠DEF=90°-∠C-
∠BAC
=90°-∠C-
(180°-∠B-∠C)
=
(∠B-∠C);
(3)有∠DEF═
(∠B-∠C),
当点E在AD内,
∠DEF=90°-∠ADF
=90°-∠C-
∠BAC
=90°-∠C-
(180°-∠B-∠C)
=
(∠B-∠C).
∠DEF=90°-∠C-
| 1 |
| 2 |
=90°-∠C-
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=10°;
(2)∠DEF=
| 1 |
| 2 |
当点E与点A重合时,
∠DEF=90°-∠C-
| 1 |
| 2 |
=90°-∠C-
| 1 |
| 2 |
=
| 1 |
| 2 |
(3)有∠DEF═
| 1 |
| 2 |
当点E在AD内,
∠DEF=90°-∠ADF
=90°-∠C-
| 1 |
| 2 |
=90°-∠C-
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,利用了三角形内角和定理,直角三角形的性质.

练习册系列答案
相关题目
设m,n为实数,则方程x2-(m+n)x+mn=0根的情况是( )
| A、有两个实数根 |
| B、无实数根 |
| C、有两个相等的实数根 |
| D、无法确定 |
2+y+3y2与1-y+2y2的差是( )
| A、3+5y2 |
| B、2y+5y2 |
| C、y2+2y+1 |
| D、y2+2y-1 |
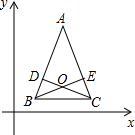 如图,在等腰△ABC中,AB=AC,BD=CE,BE、CD交于点O,BC∥x轴.已知A(3,5),B(1,1),D(2,3),则点O坐标为
如图,在等腰△ABC中,AB=AC,BD=CE,BE、CD交于点O,BC∥x轴.已知A(3,5),B(1,1),D(2,3),则点O坐标为 如图,矩形ABCD中,AB=8,BC=10,将△ADC沿着AC折叠,使点D到点D′,求重叠部分△AEC的面积.
如图,矩形ABCD中,AB=8,BC=10,将△ADC沿着AC折叠,使点D到点D′,求重叠部分△AEC的面积. 如图所示,点E、F分别是□ABCD的边BC和CD上的点,若CE=
如图所示,点E、F分别是□ABCD的边BC和CD上的点,若CE= 如图,在等腰梯形ABCD中,AD∥BC,BC=3AD,AD=1,∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF=
如图,在等腰梯形ABCD中,AD∥BC,BC=3AD,AD=1,∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF=