题目内容
 如图,在等腰梯形ABCD中,AD∥BC,BC=3AD,AD=1,∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF=
如图,在等腰梯形ABCD中,AD∥BC,BC=3AD,AD=1,∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF=考点:等腰梯形的性质,勾股定理
专题:
分析:首先理解题意,得出此题应该分两种情况进行分析,分别是AB=AE,AB=BE,从而得到最后答案.
解答:解:如图1,作AM⊥BC,DN⊥BC,垂足分别为M、N.
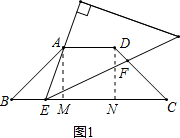
根据已知条件可得,BM=(BC-AD)÷2,
在直角三角形ABM中,cosB=
,
则AB=(BC-AD)÷2÷cosB=
.
①当AB=AE′时,如,2,

∠B=45°,∠AE′B=45°,
∴AE′=AB=
,
则在Rt△ABE′中,BE′=
AB=2,
故E′C=3-2=1.
易得△FE′C为等腰直角三角形,
故CF=
E′C=
;
②当AB=BE″时,如图3,

∵AB=
,
∴BE″=
,
∵∠AE″B=∠BAE″=(180°-45°)÷2=67.5°,
∴∠FE″C=180°-45°-67.5°=67.5°,
∴∠CFE″=180°-∠C-∠FE″C=67.5°,
∵△E″CF为等腰三角形,
∴CF=CE″=CB-BE″=3-
;
综上所述,CF的长为
或3-
.
故答案为:
或3-
.

根据已知条件可得,BM=(BC-AD)÷2,
在直角三角形ABM中,cosB=
| BM |
| AB |
则AB=(BC-AD)÷2÷cosB=
| 2 |
①当AB=AE′时,如,2,

∠B=45°,∠AE′B=45°,
∴AE′=AB=
| 2 |
则在Rt△ABE′中,BE′=
| 2 |
故E′C=3-2=1.
易得△FE′C为等腰直角三角形,
故CF=
| 2 |
| 2 |
②当AB=BE″时,如图3,

∵AB=
| 2 |
∴BE″=
| 2 |
∵∠AE″B=∠BAE″=(180°-45°)÷2=67.5°,
∴∠FE″C=180°-45°-67.5°=67.5°,
∴∠CFE″=180°-∠C-∠FE″C=67.5°,
∵△E″CF为等腰三角形,
∴CF=CE″=CB-BE″=3-
| 2 |
综上所述,CF的长为
| 2 |
| 2 |
故答案为:
| 2 |
| 2 |
点评:本题主要考查对等腰三角形的性质和判定,等腰梯形的性质,勾股定理,三角形的内角和定理等知识点的理解和掌握,能求出CE的长是解此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
下列各组图形有可能不相似的是( )
| A、各有一个角是50°的两个等腰三角形 |
| B、各有一个角是100°的两个等腰三角形 |
| C、各有一个角是50°的两个直角三角形 |
| D、两个等腰直角三角形 |
已知直角三角形的两边分别为3和6,则第三边长为( )
A、3
| ||||
B、3
| ||||
C、3
| ||||
D、3
|
如图,函数y=
与y=kx+2在同一坐标系中,图象只能是下图的( )
| k |
| x |
A、 |
B、 |
C、 |
D、 |
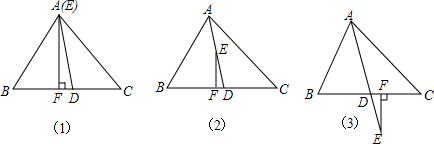
 如图,已知∠1=∠2,∠3=∠4,D是AE上任意一点,求证:DB=DC.
如图,已知∠1=∠2,∠3=∠4,D是AE上任意一点,求证:DB=DC.