题目内容
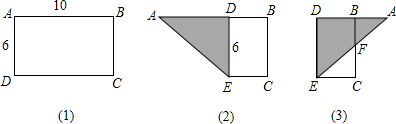
 如图,矩形ABCD中,AB=8,BC=10,将△ADC沿着AC折叠,使点D到点D′,求重叠部分△AEC的面积.
如图,矩形ABCD中,AB=8,BC=10,将△ADC沿着AC折叠,使点D到点D′,求重叠部分△AEC的面积.考点:翻折变换(折叠问题)
专题:
分析:根据翻折的性质可得∠CAD=∠CAE,再根据两直线平行,内错角相等可得∠CAD=∠ACE,然后求出∠CAE=∠ACE,再根据等角对等边可得AE=CE,设AE=CE=x,表示出BE,然后在Rt△ABE中利用勾股定理列方程求出x,再根据三角形的面积公式列式计算即可得解.
解答:解:∵△ADC沿着AC折叠,
∴∠CAD=∠CAE,
∵矩形对边AD∥BC,
∴∠CAD=∠ACE,
∴∠CAE=∠ACE,
∴AE=CE,
设AE=CE=x,则BE=10-x,
在Rt△ABE中,AB2+BE2=AE2,
即82+(10-x)2=x2,
解得x=
,
所以,△AEC的面积=
×
×8=
.
∴∠CAD=∠CAE,
∵矩形对边AD∥BC,
∴∠CAD=∠ACE,
∴∠CAE=∠ACE,
∴AE=CE,
设AE=CE=x,则BE=10-x,
在Rt△ABE中,AB2+BE2=AE2,
即82+(10-x)2=x2,
解得x=
| 41 |
| 5 |
所以,△AEC的面积=
| 1 |
| 2 |
| 41 |
| 5 |
| 164 |
| 5 |
点评:本题考查了翻折变换的性质,勾股定理,三角形的面积,熟记性质并利用勾股定理列方程求出CE的长度是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形中为圆柱体的是( )
A、 |
B、 |
C、 |
D、 |
下列各组图形有可能不相似的是( )
| A、各有一个角是50°的两个等腰三角形 |
| B、各有一个角是100°的两个等腰三角形 |
| C、各有一个角是50°的两个直角三角形 |
| D、两个等腰直角三角形 |