题目内容
 如图所示,点E、F分别是□ABCD的边BC和CD上的点,若CE=
如图所示,点E、F分别是□ABCD的边BC和CD上的点,若CE=| 1 |
| 4 |
考点:正方形的性质,勾股定理,勾股定理的逆定理
专题:证明题
分析:设正方形的边长为4a,根据CE=
CB,且CF=DF,则CE=a,BE=3a,CF=DF=2a,根据勾股定理得出AE2=AB2+BE2=(4a)2+(3a)2=25a2,EF2=CE2+CF2=a2+(2a)2=5a2,AF2=AD2+DF2=(4a)2+(2a)2=20a2,从而证得AE2=EF2+AF2,即可证得△AFE是直角三角形.
| 1 |
| 4 |
解答:解:设正方形的边长为4a,
∵CE=
CB,且CF=DF,
∴CE=a,BE=3a,CF=DF=2a,
∵四边形ABCD是正方形,
∴∠B=∠C=∠D=90°,
∴AE2=AB2+BE2=(4a)2+(3a)2=25a2,
EF2=CE2+CF2=a2+(2a)2=5a2,
AF2=AD2+DF2=(4a)2+(2a)2=20a2,
∴AE2=EF2+AF2,
∴△AEF是直角三角形.
∵CE=
| 1 |
| 4 |
∴CE=a,BE=3a,CF=DF=2a,
∵四边形ABCD是正方形,
∴∠B=∠C=∠D=90°,
∴AE2=AB2+BE2=(4a)2+(3a)2=25a2,
EF2=CE2+CF2=a2+(2a)2=5a2,
AF2=AD2+DF2=(4a)2+(2a)2=20a2,
∴AE2=EF2+AF2,
∴△AEF是直角三角形.
点评:本题考查了正方形的性质,勾股定理及其逆定理,熟练掌握性质、定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(1)在数轴上画出表示-3、-2、0、5数的点:
(2)用“<”号把数-3、-2、0、5连接为 .
(3)结论:在数轴上的两个点中,右边的点表示的数 左边的点表示的数,正数都 0,负数都 0,正数 负数.
(2)用“<”号把数-3、-2、0、5连接为
(3)结论:在数轴上的两个点中,右边的点表示的数
下列图形中为圆柱体的是( )
A、 |
B、 |
C、 |
D、 |
如图,函数y=
与y=kx+2在同一坐标系中,图象只能是下图的( )
| k |
| x |
A、 |
B、 |
C、 |
D、 |
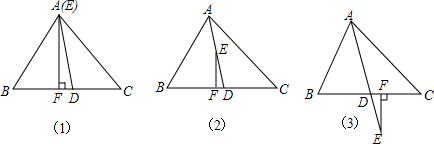
 如图,已知∠1=∠2,∠3=∠4,D是AE上任意一点,求证:DB=DC.
如图,已知∠1=∠2,∠3=∠4,D是AE上任意一点,求证:DB=DC.