题目内容
6. 如图,已知DE∥FG∥BC,且GA:AD:DB=3:4:2,则S△AGF:S△ADE:S△ABC的值是( )
如图,已知DE∥FG∥BC,且GA:AD:DB=3:4:2,则S△AGF:S△ADE:S△ABC的值是( )| A. | 3:4:2 | B. | 3:4:6 | C. | 9:16:20 | D. | 9:16:36 |
分析 由DE∥FG∥BC,可证得△AGF∽△ADE∽△ABC,又由GA:AD:DB=3:4:2,根据相似三角形的面积比等于相似比的平方,求得答案.
解答 解:∵DE∥FG∥BC,
∴△AGF∽△ADE∽△ABC,
∵GA:AD:DB=3:4:2,
∴GA:AD:AB=3:4:6,
∴S△AGF:S△ADE:S△ABC=9:16:36.
故选D.
点评 此题考查了相似三角形的判定与性质.注意求得各相似三角形的相似比是关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
17.下列各数中,比-1小的数是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
11.在$\sqrt{16}$,$\frac{π}{2}$,-$\sqrt{3}$,0,$\frac{22}{7}$,0.121221222,$\root{3}{-8}$中是有理数有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18. 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC上一点,现将纸片沿直线AD折叠,使点C落在斜边AB上的点E处,则CD等于( )
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC上一点,现将纸片沿直线AD折叠,使点C落在斜边AB上的点E处,则CD等于( )
 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC上一点,现将纸片沿直线AD折叠,使点C落在斜边AB上的点E处,则CD等于( )
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC上一点,现将纸片沿直线AD折叠,使点C落在斜边AB上的点E处,则CD等于( )| A. | 2.4cm | B. | 3cm | C. | 4cm | D. | 4.8cm |
15.已知点P是线段AB上的一点,且AP>PB,AP2=PB•AB,若AB=4,那么AP的长是( )
| A. | 2.472 | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | 0.618 | D. | $2\sqrt{5}-2$ |
16.若a=-0.42,b=-4-2,c=(-$\frac{1}{4}$)-2,d=(-$\frac{1}{4}$)0,则a,b,c,d的大小关系是( )
| A. | a<b<d<c | B. | b<a<d<c | C. | a<d<c<b | D. | c<a<d<b |
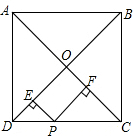 如图所示,在正方形ABCD中,若对角线的长为10cm,P是CD上任意一点,过点P分别作PE⊥BD,PF⊥AC,垂足分别为E,F,则PE+PF=5cm.
如图所示,在正方形ABCD中,若对角线的长为10cm,P是CD上任意一点,过点P分别作PE⊥BD,PF⊥AC,垂足分别为E,F,则PE+PF=5cm.