题目内容
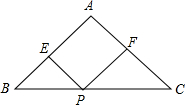 如图,△ABC中,AB=AC,BC=20cm,点P在BC边上从点B开始以2cm/s速度向点C运动,过点P作PE∥AC交AB于点E,PF∥AB交AC于点F.问:四边形AEPF是否可能是菱形?如有可能,是在什么时刻?如不可能,请说明理由.
如图,△ABC中,AB=AC,BC=20cm,点P在BC边上从点B开始以2cm/s速度向点C运动,过点P作PE∥AC交AB于点E,PF∥AB交AC于点F.问:四边形AEPF是否可能是菱形?如有可能,是在什么时刻?如不可能,请说明理由.考点:菱形的判定
专题:动点型
分析:由条件可知四边形AEPF为平行四边形,当PE=PF时,可知其为菱形,此时可证得△BPE≌△CPF,可得BP=CP=10,可求得时间,即把t=5当成条件证明四边形AEPF为菱形即可.
解答:解:当t=5s时四边开AEPF为菱形,理由如下:
当t=5时,BP=CP=10,
∵PE∥AC,PF∥AB
∴四边形AEPF为平行四边形,且∠BEP=∠A,∠PFC=∠A,
∴∠BEP=∠PFC,
∵AB=AC,
∴∠B=∠C,
在△BEP和△CFP中,
,
∴△BPE≌△CPF(AAS),
∴PE=PF,
∴四边形AEPF为菱形.
当t=5时,BP=CP=10,
∵PE∥AC,PF∥AB
∴四边形AEPF为平行四边形,且∠BEP=∠A,∠PFC=∠A,
∴∠BEP=∠PFC,
∵AB=AC,
∴∠B=∠C,
在△BEP和△CFP中,
|
∴△BPE≌△CPF(AAS),
∴PE=PF,
∴四边形AEPF为菱形.
点评:本题主要考查菱形的判定,掌握菱形的判定方法是解题的关键,即可以先证其为平行四边形,再加一组邻边相等或对角线互相垂直.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,要建立一个形状是直角梯形的存料场,其中两边是夹角为150°的两面墙,另外两边是总长为30m的篱笆,问篱笆两边各是多少米时,存料场的面积最大?最大面积是多少?
如图,要建立一个形状是直角梯形的存料场,其中两边是夹角为150°的两面墙,另外两边是总长为30m的篱笆,问篱笆两边各是多少米时,存料场的面积最大?最大面积是多少? 折叠三角形纸片ABC,使点A落在BC边上的点F,且折痕DE平行BC,若∠B=50°,求∠BDF的度数,并说明理由.
折叠三角形纸片ABC,使点A落在BC边上的点F,且折痕DE平行BC,若∠B=50°,求∠BDF的度数,并说明理由.