题目内容
若x<0,x+y>0,化简:|y-x+2|-|x-y-1|.
考点:整式的加减,绝对值
专题:
分析:由x<0,x+y>0得出y>0,所以|y-x+2|=y-x+2,|x-y-1|=-(x-y-1),然后代入去括号合并同类项即可.
解答:解:∵x<0,x+y>0,
∴y>0,|y-x+2|=y-x+2,|x-y-1|=-(x-y-1),
∴|y-x+2|-|x-y-1|=(y-x+2)+(x-y-1)=1.
∴y>0,|y-x+2|=y-x+2,|x-y-1|=-(x-y-1),
∴|y-x+2|-|x-y-1|=(y-x+2)+(x-y-1)=1.
点评:本题考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.利用绝对值的性质去掉绝对值的符号是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
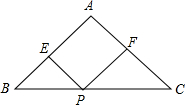 如图,△ABC中,AB=AC,BC=20cm,点P在BC边上从点B开始以2cm/s速度向点C运动,过点P作PE∥AC交AB于点E,PF∥AB交AC于点F.问:四边形AEPF是否可能是菱形?如有可能,是在什么时刻?如不可能,请说明理由.
如图,△ABC中,AB=AC,BC=20cm,点P在BC边上从点B开始以2cm/s速度向点C运动,过点P作PE∥AC交AB于点E,PF∥AB交AC于点F.问:四边形AEPF是否可能是菱形?如有可能,是在什么时刻?如不可能,请说明理由. 如图,AB为⊙O直径,点P在BA延长线上,点D在⊙O上,C是PD与⊙O的交点.已知PA=3,PB=13,∠P=30°,求CD的长.
如图,AB为⊙O直径,点P在BA延长线上,点D在⊙O上,C是PD与⊙O的交点.已知PA=3,PB=13,∠P=30°,求CD的长.