题目内容
某商店购进一批单价为18元的商品,如果以单价20元出售,那么一个星期可售出100件.根据销售经验,提高销售单价会导致销售量减少,即当销售单价每提高1元,销售量相应减少10件,如何提高销售单价,才能在一个星期内获得最大利润?最大利润是多少?
考点:二次函数的应用
专题:
分析:设售价提高x元,总利润为W元,则销量为(100-10x)件,根据利润=数量×每件的利润建立W与x的关系式,由二次函数的性质就可以求出结论.
解答:解:设售价提高x元,总利润为W元,由题意,得
W=(20+x-18)(100-10x),
W=-10(x-4)2+360.
∴a=-10<0,
∴x=4时,W最大=360元.
答:售价提高4元时,才能在一个星期内获得最大利润,最大利润是360元.
W=(20+x-18)(100-10x),
W=-10(x-4)2+360.
∴a=-10<0,
∴x=4时,W最大=360元.
答:售价提高4元时,才能在一个星期内获得最大利润,最大利润是360元.
点评:本题考查了销售问题的数量关系利润=数量×每件的利润的运用,二次函数的性质的运用,顶点式的运用,解答时求出函数的解析式是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知五个数2,3,x,5,7的平均数为6,四个2,3,x,y的平均数为7,则y=( )
| A、10 | B、9 | C、8 | D、7 |
 如图,在△ABC中,AD⊥BC,BE⊥AC,D、E分别为垂足,求证:△DEF∽△BAF.
如图,在△ABC中,AD⊥BC,BE⊥AC,D、E分别为垂足,求证:△DEF∽△BAF. 如图,Rt△ABC的两条直角边BC=15cm,AC=20cm,斜边AB上的高为CD.若以C为圆心,分别以r1=11cm,r2=12cm,r3=13cm为半径作圆,试判断D点与这三个圆的位置关系.
如图,Rt△ABC的两条直角边BC=15cm,AC=20cm,斜边AB上的高为CD.若以C为圆心,分别以r1=11cm,r2=12cm,r3=13cm为半径作圆,试判断D点与这三个圆的位置关系.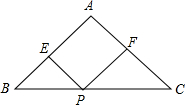 如图,△ABC中,AB=AC,BC=20cm,点P在BC边上从点B开始以2cm/s速度向点C运动,过点P作PE∥AC交AB于点E,PF∥AB交AC于点F.问:四边形AEPF是否可能是菱形?如有可能,是在什么时刻?如不可能,请说明理由.
如图,△ABC中,AB=AC,BC=20cm,点P在BC边上从点B开始以2cm/s速度向点C运动,过点P作PE∥AC交AB于点E,PF∥AB交AC于点F.问:四边形AEPF是否可能是菱形?如有可能,是在什么时刻?如不可能,请说明理由.