题目内容
已知a2+a+1=0,求a1000+a2001+a3002的值.
考点:因式分解的应用
专题:
分析:由a2+a+1=0,则a2=-a-1,再计算出a3=1,a4=a,接着利用积的乘方计算出a1001=a2,然后利用因式分解得到原式=a1000(1+a1001+a2002),再利用幂的乘方进行计算,可得到原式=a1000(1+a2+a),则利用整体代入的方法计算即可.
解答:解:∵a2+a+1=0,
∴a2=-a-1,
∴a3=a(-a-1)=-a2-a=a+1-a=1,
a4=a,
∴a1001=a3×333+2=(a3)333•a2=a2,
∴原式=a1000(1+a1001+a2002)
=a1000[1+a1001+(a1001)2]
=a1000(1+a2+a4)
=a1000(1+a2+a)
=a1000[•0
=0.
∴a2=-a-1,
∴a3=a(-a-1)=-a2-a=a+1-a=1,
a4=a,
∴a1001=a3×333+2=(a3)333•a2=a2,
∴原式=a1000(1+a1001+a2002)
=a1000[1+a1001+(a1001)2]
=a1000(1+a2+a4)
=a1000(1+a2+a)
=a1000[•0
=0.
点评:本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
相关题目
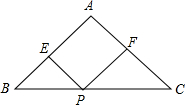 如图,△ABC中,AB=AC,BC=20cm,点P在BC边上从点B开始以2cm/s速度向点C运动,过点P作PE∥AC交AB于点E,PF∥AB交AC于点F.问:四边形AEPF是否可能是菱形?如有可能,是在什么时刻?如不可能,请说明理由.
如图,△ABC中,AB=AC,BC=20cm,点P在BC边上从点B开始以2cm/s速度向点C运动,过点P作PE∥AC交AB于点E,PF∥AB交AC于点F.问:四边形AEPF是否可能是菱形?如有可能,是在什么时刻?如不可能,请说明理由.