题目内容
12．
已知有理数a，b，c在数轴上对应点的位置如图所示，化简：|b-c|-2|c-a|+|b+c|=-2a．
分析 根据数轴先得出b-c，c-a，b+c的符号，再去绝对值，根据绝对值的性质去绝对值进行计算即可．
解答 解：由图得，b-c＞0，c-a＜0，b+c＜0，
则原式=b-c+2（c-a）-（b+c）
=b-c+2c-2a-b-c
=-2a．
故答案为-2a．
点评 本题考查了整式的加减，以及绝对值、数轴，解决此类题目的关键是熟记绝对值的性质，熟练运用合并同类项的法则，这是各地中考的常考点．
练习册系列答案
相关题目
20．
如图所示，△ABC∽△ACD，且AB=10cm，AC=8cm，则AD的长是（ ）
如图所示，△ABC∽△ACD，且AB=10cm，AC=8cm，则AD的长是（ ）| A． | 6.4cm | B． | 6cm | C． | 2cm | D． | 4cm |
17．
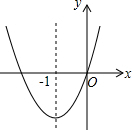如图，已知经过原点的抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=-1，下列结论中：?①ab＞0，?②a+b+c＞0，?③当-2＜x＜0时，y＜0，④2a-b=0，正确的个数是（ ）
如图，已知经过原点的抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=-1，下列结论中：?①ab＞0，?②a+b+c＞0，?③当-2＜x＜0时，y＜0，④2a-b=0，正确的个数是（ ）| A． | 1个 | B． | 2个 | C． | 3 个 | D． | 4个 |
4．观察下列等式：
第一个等式：a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$；
第二个等式：a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$；
第三个等式：a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$；
第四个等式：a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$．
按上述规律，则式子a1+a2+a3+…+a22的结果为（ ）
第一个等式：a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$；
第二个等式：a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$；
第三个等式：a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$；
第四个等式：a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$．
按上述规律，则式子a1+a2+a3+…+a22的结果为（ ）
| A． | $\frac{1}{2}-\frac{1}{{21×{2^{21}}}}$ | B． | $\frac{1}{2}-\frac{1}{{22×{2^{22}}}}$ | C． | $\frac{1}{2}-\frac{1}{{23×{2^{23}}}}$ | D． | $\frac{1}{2}-\frac{1}{{24×{2^{24}}}}$ |
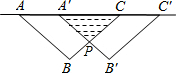如图，把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时，它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$．若AB=$\sqrt{2}$cm，则它移动的距离AA′=1cm．