题目内容
17.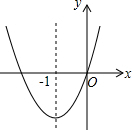 如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0,④2a-b=0,正确的个数是( )
如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0,④2a-b=0,正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3 个 | D. | 4个 |
分析 ①由抛物线的开口向上,对称轴在y轴左侧,判断a,b与0的关系,得到?ab>0;
②由x=1时,得到y=a+b+c>0;
③根据对称轴和抛物线与x轴的一个交点,得到另一个交点,然后根据图象确定答案即可;
④根据对称轴x=-$\frac{b}{2a}$=-1,即可得到2a-b=0.
解答 解:①∵抛物线的开口向上,
∴a>0,
∵对称轴在y轴的左侧,
∴b>0
∴?ab>0;故①正确;
②∵观察图象知;当x=1时y=a+b+c>0,
∴②正确;
③∵抛物线的对称轴为x=-1,与x轴交于(0,0),
∴另一个交点为(-2,0),
∴当-2<x<0时,y<0;故③正确;
④∵抛物线的对称轴为x=-1,
∴-$\frac{b}{2a}$=-1,即$\frac{b}{2a}$=1,
∴b=2a,
∴2a-b=0;故④正确;
故选D.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.抛物线y=ax2经过点(1,3),则a的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 9 |
 已知有理数a,b,c在数轴上对应点的位置如图所示,化简:|b-c|-2|c-a|+|b+c|=-2a.
已知有理数a,b,c在数轴上对应点的位置如图所示,化简:|b-c|-2|c-a|+|b+c|=-2a.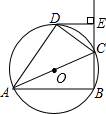 如图.四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC于E,CD平分∠ACE.
如图.四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC于E,CD平分∠ACE.