题目内容
5. 如图,四边形ABCD是平行四边形,点E在BA的延长线上,∠ECA=∠D,AD=AE=3,CE=5,求AC的长.
如图,四边形ABCD是平行四边形,点E在BA的延长线上,∠ECA=∠D,AD=AE=3,CE=5,求AC的长.
分析 由四边形ABCD是平行四边形,∠ECA=∠D,易证得∠ECA=∠B,又由∠E是公共角,证得△EAC∽△ECB,然后由相似三角形的对应边成比例,可得AC:BC=AE:CE=CE:BE,代入数据即可得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴BC=AD,CD∥AB,AD∥BC,
∴∠D=∠DAE=∠B,
∵∠ECA=∠D,
∴∠ECA=∠B,
∵∠E=∠E,
∴△EAC∽△ECB,
∴AC:BC=AE:CE=CE:BE,
∴BE=$\frac{C{E}^{2}}{AE}$=$\frac{25}{3}$,AC•BE=CE•AD,
∴AC=$\frac{CE•AD}{BE}$=$\frac{5×3}{\frac{25}{3}}$=$\frac{9}{5}$.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
16.下列二次根式中是最简二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{5}$ | D. | $\sqrt{\frac{3}{2}}$ |
17.a(x-y)与ay-ax的公因式是( )
| A. | a(x-y) | B. | ay+ax | C. | a | D. | x-y |
 如图,已知线段a,b,用直尺和圆规画图.
如图,已知线段a,b,用直尺和圆规画图.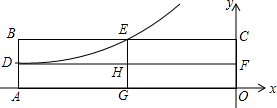 如图,矩形OABC的两边AB,BC分别与双曲线y=$\frac{k}{x}$(k<0)交于D,E两点,DF⊥y轴于F点,EG⊥x轴于G点,若矩形OGHF的面积为1,矩形OABC的面积为9,则k的值为-3.
如图,矩形OABC的两边AB,BC分别与双曲线y=$\frac{k}{x}$(k<0)交于D,E两点,DF⊥y轴于F点,EG⊥x轴于G点,若矩形OGHF的面积为1,矩形OABC的面积为9,则k的值为-3. 在一块空旷的草地上有一根拄子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示.
在一块空旷的草地上有一根拄子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示.