题目内容
13. 如图,在矩形ABCD中,AB=8,BC=12,点E为BC的中点.连接AE,将△ABE沿AE折叠,点B落在点F处,连接CF,现将△CEF绕点E顺时针旋转α角(其中0°≤α≤180°)得到△EC1F1,旋转过程中,直线C1F1分别交射线EC、射线AE于点M、N,当EM=EN时,则CM=6-$\frac{12\sqrt{5}}{5}$.
如图,在矩形ABCD中,AB=8,BC=12,点E为BC的中点.连接AE,将△ABE沿AE折叠,点B落在点F处,连接CF,现将△CEF绕点E顺时针旋转α角(其中0°≤α≤180°)得到△EC1F1,旋转过程中,直线C1F1分别交射线EC、射线AE于点M、N,当EM=EN时,则CM=6-$\frac{12\sqrt{5}}{5}$.
分析 如图作EK⊥FC,EJ⊥MN垂足分别为K、J,延长JE交AB于G,作GH⊥AE垂足为H,根据条件可以求出EK=EJ=$\frac{24}{5}$,BG=3,EG=3$\sqrt{5}$,利用△EBG∽△EJM求出EM,即可解决问题.
解答 解:如图作EK⊥FC,EJ⊥MN垂足分别为K、J,延长JE交AB于G,作GH⊥AE垂足为H.
∵四边形ABCD是矩形,AB=8,BC=12,BE=EC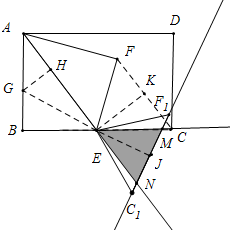
∴∠B=90°,BE=6,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=10,
∵△AEF是△AEB翻折,
∴∠B=∠AFE=90°,∠BAE=∠EAF,
∴∠BAF+∠BEF=180°,
∵∠BEF+∠FEC=180°,
∴∠FEC=∠BAF,
∵EF=EC,EK⊥FC,
∴∠FEK=∠CEK,
∴∠BAE=∠CEK,
∵∠ABE=∠EKF,
∴△ABE∽△EKF,
∴$\frac{AE}{EF}=\frac{AB}{EK}$,即$\frac{10}{6}=\frac{8}{EK}$,
∴EK=$\frac{24}{5}$,
∵△EC1F1是由△EFC旋转,EK⊥FC,EJ⊥F1C1,
∴EJ=EK=$\frac{24}{5}$,
∵EM=EN,EJ⊥MN,
∴∠MEJ=∠NEJ,
∵∠GEB=∠MEJ,∠GEH=∠NEJ,
∴∠GEB=∠GEH,∵GB⊥BE,GH⊥HE,
∴GB=GH,设GB=GH=x,
在RT△AGH中,由AG2=GH2+AH2,得(8-x)2=x2+42,
∴x=3,
∴BG=GH=3,AG=5,
∴EG=$\sqrt{B{G}^{2}+B{E}^{2}}$=,3$\sqrt{5}$,
∵∠BEG=∠MEJ,∠B=∠EJM=90°,
∴△EBG∽△EJM,
∴$\frac{EG}{EM}=\frac{BE}{EJ}$,
∴$\frac{3\sqrt{5}}{EM}=\frac{6}{\frac{24}{5}}$,
∴EM=$\frac{12\sqrt{5}}{5}$,
∴CM=EC-EM=6-$\frac{12\sqrt{5}}{5}$.
故答案为6-$\frac{12\sqrt{5}}{5}$.
点评 本题考查了翻折和旋转的有关性质、等腰三角形的性质、角平分线的性质、相似三角形的判定和性质、勾股定理等知识,构造三角形相似是解题关键.

| A. | 0 | B. | $\sqrt{16}$ | C. | $\frac{22}{7}$ | D. | π |
 如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=2BD,则$\frac{CF}{CB}$的值为( )
如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=2BD,则$\frac{CF}{CB}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
 如图,D、E分别是△ABC的边AB、AC上的中点,则S△ADE:S四边形DBCE=( )
如图,D、E分别是△ABC的边AB、AC上的中点,则S△ADE:S四边形DBCE=( )| A. | 2:5 | B. | 1:3 | C. | 3:5 | D. | 3:2 |
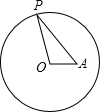 如图,点A在半径为3的⊙O内,OA=$\sqrt{3}$,P为⊙O上一点,当∠OPA取最大值时,PA的长等于$\sqrt{6}$.
如图,点A在半径为3的⊙O内,OA=$\sqrt{3}$,P为⊙O上一点,当∠OPA取最大值时,PA的长等于$\sqrt{6}$. 如图,将边长为4的正方形ABCD折叠,使B点落在边AD上,记作B′(不与A、D重合)、EF为折痕,设AB′=x.
如图,将边长为4的正方形ABCD折叠,使B点落在边AD上,记作B′(不与A、D重合)、EF为折痕,设AB′=x. 如图,点A,O,D三点在一条直线上,∠AOB=20°,∠BOC=3∠COD.
如图,点A,O,D三点在一条直线上,∠AOB=20°,∠BOC=3∠COD. 如图,以扇形AOB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),∠AOB=45°.现从$-2,-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2}$中随机选取一个数记为a,则a的值既使得抛物线$y=\frac{1}{2}{x^2}+a$与扇形AOB的边界有公共点,又使得关于x的方程$\frac{ax+1}{x-2}=-1$的解是正数的概率是$\frac{1}{6}$.
如图,以扇形AOB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),∠AOB=45°.现从$-2,-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2}$中随机选取一个数记为a,则a的值既使得抛物线$y=\frac{1}{2}{x^2}+a$与扇形AOB的边界有公共点,又使得关于x的方程$\frac{ax+1}{x-2}=-1$的解是正数的概率是$\frac{1}{6}$.