题目内容
19. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )
如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据网格中的数据求出AB,AC,BC的长,求出三边之比,利用三边对应成比例的两三角形相似判断即可.
解答 解:由勾股定理得:AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,BC=2,AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴AC:BC:AB=1:$\sqrt{2}$:$\sqrt{5}$,
A、三边之比为1:$\sqrt{5}$:2$\sqrt{2}$,图中的三角形(阴影部分)与△ABC不相似;
B、三边之比:1:$\sqrt{2}$:$\sqrt{5}$,图中的三角形(阴影部分)与△ABC相似;
C、三边之比为$\sqrt{2}$:$\sqrt{5}$:3,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2:$\sqrt{5}$:$\sqrt{13}$,图中的三角形(阴影部分)与△ABC不相似.
故选B.
点评 此题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解本题的关键.

练习册系列答案
相关题目
9.若|x|=3,|y|=4,且|x-y|=y-x,则xy的值为( )
| A. | -1 | B. | -12 | C. | 12 | D. | 12或-12 |
4. 如图所示,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC,∠ACB,AD、CE相交于点O,下列结论不一定正确的是( )
如图所示,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC,∠ACB,AD、CE相交于点O,下列结论不一定正确的是( )
 如图所示,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC,∠ACB,AD、CE相交于点O,下列结论不一定正确的是( )
如图所示,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC,∠ACB,AD、CE相交于点O,下列结论不一定正确的是( )| A. | ∠AOC=120° | B. | OE=OD | ||
| C. | BE=BD | D. | S△AEO+S△CDO=S△ACO |
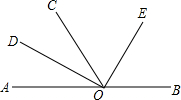 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,请求出∠AOD、∠COE、∠BOC、∠BOE的度数.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,请求出∠AOD、∠COE、∠BOC、∠BOE的度数.