题目内容
7.一个机器人从数轴的原点出发,沿数轴的正方向,以每进4步接着后退3步的程序运动,该机器人每秒前进或后退1步,并且每步的距离为1个单位长度,xn表示第n秒机器人在数轴上的位置所对应的数(如x4=4,x3=3,x?=1),则x2016-x2014=-2.分析 根据每进4步接着后退3步,每秒前进或后退1步,可知每7秒前进1步,由此可以得出第n秒时机器人在数轴上的位置,从而可以解答本题.
解答 解:∵一个机器人从数轴的原点出发,沿数轴的正方向,以每进4步接着后退3步的程序运动,每秒前进或后退1步,并且每步的距离为1个单位长度,
∴该机器人每7秒前进1步,
2016=7×288,故第2016秒对应的数是288,第2014秒对应的数是290
∴x2016-x2014=288-290=-2,
故答案为:-2.
点评 本题考查数轴,解题的关键是明确数轴的特点,可以发现机器人运动的规律.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
15.已知点A(m+2,3m-6)在第一象限角平分线上,则m的值为( )
| A. | 2 | B. | -1 | C. | 4 | D. | -2 |
17. 如图,∠C=∠D=90°,AD=BC,AC与BD相交于O,则下列结论中不正确的是( )
如图,∠C=∠D=90°,AD=BC,AC与BD相交于O,则下列结论中不正确的是( )
 如图,∠C=∠D=90°,AD=BC,AC与BD相交于O,则下列结论中不正确的是( )
如图,∠C=∠D=90°,AD=BC,AC与BD相交于O,则下列结论中不正确的是( )| A. | ∠CAB与∠DBA互余 | B. | ∠DAB=∠CBA | C. | AC=BD | D. | △DAO≌△CBO |
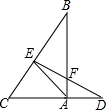 如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于点E,交CA的延长线于D,交AB于点F,求证:AE2=EF•ED.
如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于点E,交CA的延长线于D,交AB于点F,求证:AE2=EF•ED. 如图,直线y=x-4与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点A,连接OA.若S△AOB:S△BOC=1:2,则k的值为12.
如图,直线y=x-4与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点A,连接OA.若S△AOB:S△BOC=1:2,则k的值为12.