题目内容
 如图,抛物线y=ax2+bx+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,其对称轴是x=1,且OB=OC.
如图,抛物线y=ax2+bx+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,其对称轴是x=1,且OB=OC.(1)求抛物线的解析式;
(2)将抛物线沿y轴平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,求t的取值范围或t的值;
(3)抛物线上是否存在点P,使∠BCP=∠BAC-∠ACO?若存在,求P点坐标;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)根据OB=OC,可得到B点的坐标,将B、C的坐标代入抛物线的解析式中,即可求得待定系数的值,从而确定该抛物线的解析式.
(2)把函数化为顶点式y=a(x-h)2+k的形式,向上平移使抛物线与x轴只有一个交点,即把解析式中的k变成0即可.
(3)取AC的中点M,过M作MN⊥AC交OC于N,连接AN则AN=CN,∠ACO=∠CAN,通过△MCN∽△OCA,求得CN的值,进而求得NO的值,从而得出tan∠NAO=
=
;当P在BC的上方时,设为P1,过B作BD⊥BC交直线CP1于D,过D作DE⊥x轴于E,通过证明△BDE∽△CBO,进而求得tan∠BCP1=tan∠NAO=
,从而确定D点的坐标,把D点代入直线CP1的解析式为y=k1x+3,求得P1点的坐标;当点P在BC下方时,设为P2(m,n),则∠BCP2=∠BCP1,延长DB交直线CP2于E,则点B是DE的中点,求得E点坐标,代入直线CP2的解析式为y=k2x+3,即可求得P2的坐标.
(2)把函数化为顶点式y=a(x-h)2+k的形式,向上平移使抛物线与x轴只有一个交点,即把解析式中的k变成0即可.
(3)取AC的中点M,过M作MN⊥AC交OC于N,连接AN则AN=CN,∠ACO=∠CAN,通过△MCN∽△OCA,求得CN的值,进而求得NO的值,从而得出tan∠NAO=
| NO |
| AO |
| 4 |
| 3 |
| 4 |
| 3 |
解答:解:(1)∵抛物线y=ax2+bx+3与y轴交于点C
∴C(0,3),
∴OC=3
∵OB=OC,
∴OB=3
∵抛物线的对称轴是x=1,
∴B(3,0),A(-1,0)
∴
解得
∴抛物线的解析式为y=-x2+2x+3;
(2)由题意,抛物线只能沿y轴向下平移
∵y=-x2+2x+3=-(x-1)2+4
∴设平移后的抛物线的解析式为y=-(x-1)2+4-t(t>0)
当原点O落在平移后的抛物线上时,把(0,0)代入得:
0=-(0-1)2+4-t,
解得t=3;
当平移后的抛物线的顶点落在x轴上时,x=1,y=0
即0=-(1-1)2+4-t,
解得t=4,
∵平移后的抛物线与线段OB有且只有一个交点
∴0<t<3或t=4
(3)取AC的中点M,过M作MN⊥AC交OC于N,连接AN
则AN=CN,
∴∠ACO=∠CAN
∵∠BCP=∠BAC-∠ACO,
∴∠BCP=∠BAC-∠CAN=∠NAO
∵∠ACO=∠NCM,∠AOC=∠CMN=90°,
∴△MCN∽△OCA,
∴
=
∴CN=
=
=
=
∴NO=CO-CN=3-
=
,
∴tan∠NAO=
=
;
当点P在BC上方时,设为P1,过B作BD⊥BC交直线CP1于D,过D作DE⊥x轴于E
∵∠OCB=∠DBE,∠BOC=∠BED=90°,
∴△BDE∽△CBO,
∴
=
=
=tan∠BCP1=tan∠NAO=
∴BE=
CO=4,DE=
BO=4,OE=3+4=7
∴D(7,4)
设直线CP1的解析式为y=k1x+3,把(7,4)代入
4=7k1+3,
∴k1=
,
∴y=
x+3
令-x2+2x+3=
x+3,
解得x1=0(舍去),x2=
∴P1(
,
),
当点P在BC下方时,设为P2(m,n),
则∠BCP2=∠BCP1
延长DB交直线CP2于E,则点B是DE的中点
∴
解得
∴E(-1,-4)
设直线CP2的解析式为y=k2x+3,把(-1,-4)代入-4=-k2+3,
∴k2=7,
∴y=7x+3
令-x2+2x+3=7x+3,
解得x1=0(舍去),x2=-5
∴P2(-5,-32)
综上所述,抛物线上存在点P,使∠BCP=∠BAC-∠ACO,
P点坐标为(
,
)或(-5,-32).
∴C(0,3),
∴OC=3
∵OB=OC,
∴OB=3
∵抛物线的对称轴是x=1,
∴B(3,0),A(-1,0)
∴
|
解得
|
∴抛物线的解析式为y=-x2+2x+3;
(2)由题意,抛物线只能沿y轴向下平移
∵y=-x2+2x+3=-(x-1)2+4
∴设平移后的抛物线的解析式为y=-(x-1)2+4-t(t>0)
当原点O落在平移后的抛物线上时,把(0,0)代入得:
0=-(0-1)2+4-t,
解得t=3;
当平移后的抛物线的顶点落在x轴上时,x=1,y=0
即0=-(1-1)2+4-t,
解得t=4,
∵平移后的抛物线与线段OB有且只有一个交点
∴0<t<3或t=4
(3)取AC的中点M,过M作MN⊥AC交OC于N,连接AN
则AN=CN,
∴∠ACO=∠CAN
∵∠BCP=∠BAC-∠ACO,
∴∠BCP=∠BAC-∠CAN=∠NAO
∵∠ACO=∠NCM,∠AOC=∠CMN=90°,
∴△MCN∽△OCA,
∴
| CM |
| CN |
| CO |
| CA |
∴CN=
| CM•CA |
| CO |
| CA2 |
| 2CO |
| 12+32 |
| 2×3 |
| 5 |
| 3 |
∴NO=CO-CN=3-
| 5 |
| 3 |
| 4 |
| 3 |
∴tan∠NAO=
| NO |
| AO |
| 4 |
| 3 |
当点P在BC上方时,设为P1,过B作BD⊥BC交直线CP1于D,过D作DE⊥x轴于E
∵∠OCB=∠DBE,∠BOC=∠BED=90°,
∴△BDE∽△CBO,
∴
| BE |
| CO |
| DE |
| BO |
| BD |
| BC |
| 4 |
| 3 |
∴BE=
| 4 |
| 3 |
| 4 |
| 3 |
∴D(7,4)
设直线CP1的解析式为y=k1x+3,把(7,4)代入
4=7k1+3,
∴k1=
| 1 |
| 7 |
∴y=
| 1 |
| 7 |
令-x2+2x+3=
| 1 |
| 7 |
解得x1=0(舍去),x2=
| 13 |
| 7 |
∴P1(
| 13 |
| 7 |
| 160 |
| 49 |
当点P在BC下方时,设为P2(m,n),
则∠BCP2=∠BCP1
延长DB交直线CP2于E,则点B是DE的中点
∴
|
解得
|
∴E(-1,-4)
设直线CP2的解析式为y=k2x+3,把(-1,-4)代入-4=-k2+3,
∴k2=7,
∴y=7x+3
令-x2+2x+3=7x+3,
解得x1=0(舍去),x2=-5
∴P2(-5,-32)
综上所述,抛物线上存在点P,使∠BCP=∠BAC-∠ACO,
P点坐标为(
| 13 |
| 7 |
| 160 |
| 49 |
点评:此题是二次函数的综合题,主要考查了二次函数解析式的确定以及相似三角形的判定和性质,对称轴顶点坐标的公式,以及函数与坐标轴交点坐标的求解方法.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
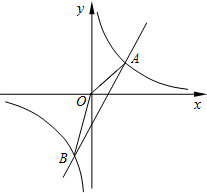 如图,已知反比例函数y1=
如图,已知反比例函数y1= 如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,1),
如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,1),