题目内容
 如图,△ABC中,BC=80mm,AH=60mm,D在AB边上,E在AC上,DE∥BC以DE为边在△ABC内作矩形DEFG,设DE=x,DG=y.
如图,△ABC中,BC=80mm,AH=60mm,D在AB边上,E在AC上,DE∥BC以DE为边在△ABC内作矩形DEFG,设DE=x,DG=y.(1)求y与x的函数关系式;
(2)当x取何值时,矩形DEFG的面积是1200mm2?.
考点:相似三角形的判定与性质,一元二次方程的应用
专题:
分析:(1)设高AH交DE于K,由矩形的性质可知:DE∥BC,进而可证明△ADE∽△ABC,利用相似三角形的性质即可求出y与x的函数关系式;
(2)利用矩形的面积公式可知:x•y=1200,由(1)可知x和y的关系,进而得到关于x的一元二次方程,解方程即可.
(2)利用矩形的面积公式可知:x•y=1200,由(1)可知x和y的关系,进而得到关于x的一元二次方程,解方程即可.
解答:解:(1)设高AH交DE于K,
∵DE∥BC,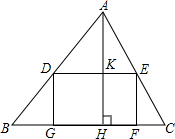
∴△ADE∽△ABC,
∴AK:AH=DE:BC,
∵DE=x,DG=y,
∴KH=y,
即AK=AH-KH,
∴y=-
x+60;
(2)∵x•y=1200,y=-
x+60∴
-
x2+60x=1200,
解得:x1=x2=40,
答:当x=40mm时,矩形DEFG的面积是1200mm2.
∵DE∥BC,

∴△ADE∽△ABC,
∴AK:AH=DE:BC,
∵DE=x,DG=y,
∴KH=y,
即AK=AH-KH,
∴y=-
| 3 |
| 4 |
(2)∵x•y=1200,y=-
| 3 |
| 4 |
-
| 3 |
| 4 |
解得:x1=x2=40,
答:当x=40mm时,矩形DEFG的面积是1200mm2.
点评:此题考查学生对相似三角形的判定与性质,一元二次方程的应用,矩形的性质,等知识点的理解和掌握,此题的关键是利用相似三角形对应边的比等于其对应高的比,然后即可求得y与x的函数关系式和最值.

练习册系列答案
相关题目
 已知:长方形ABCD中有两个小正方形甲和乙,甲的面积为2,乙的面积为9
已知:长方形ABCD中有两个小正方形甲和乙,甲的面积为2,乙的面积为9 如图,D是Rt△ABC的斜边AB的中点,E是BC上的一点,且BE=
如图,D是Rt△ABC的斜边AB的中点,E是BC上的一点,且BE=