题目内容
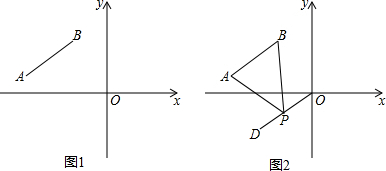
13.如图1,已知线段AB两个端点坐标分别为A(a,1),B(-2,b),且a、b满足:$\sqrt{a+5}$+$\sqrt{b-3}$=0.(1)则a=-5,b=3;
(2)如图2,将线段BA平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点.求△PAB的面积.
分析 (1)根据二次根式的性质可得,a+5=0,b-3=0,可得:a=-5,b=3;
(2)由(1)得:A(-5,1),B(-2,3),计算出AB,再求出直线AB的解析式,求出点P到直线AB的距离,即可求出△PAB的面积.
解答 解:(1)∵$\sqrt{a+5}+\sqrt{b-3}$=0,
∴a+5=0,b-3=0,
∴a=-5,b=3.
故答案为:-5,3.
(2)由(1)得:A(-5,1),B(-2,3),
AB=$\sqrt{(-5+2)^{2}+(1-3)^{2}}$=$\sqrt{13}$,
设过点A,B直线的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-5k+b=1}\\{-2k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=\frac{13}{3}}\end{array}\right.$,
∴y=$\frac{2}{3}x+\frac{13}{3}$,
即2x-3y+13=0,
点P到直线AB的距离为:$\frac{|2m-3n+13|}{\sqrt{{2}^{2}+{3}^{2}}}=\frac{|2m-3n+13|}{\sqrt{13}}$,
∴△PAB的面积为:$\frac{1}{2}×\sqrt{13}×\frac{|2m-3n+13|}{\sqrt{13}}$=$\frac{|2m-3n+13|}{2}$.
点评 本题考查了坐标与图形的性质,解决本题的关键是求出点A,点B的坐标.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
16.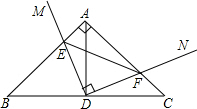 如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
 如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )| A. | ①②④ | B. | ②③④ | C. | ①②③ | D. | ①②③④ |
17.已知m,n均不等于0,且m-n=2mn,则$\frac{2}{m}-\frac{2}{n}$的值是( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
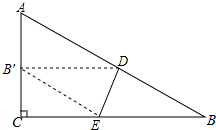 如图是一张直角三角形纸片,∠C=90°,点D在边AB上,若将三角形纸片沿直线DE折叠,使点B落在AC边上,记作点B′,连接B′E.
如图是一张直角三角形纸片,∠C=90°,点D在边AB上,若将三角形纸片沿直线DE折叠,使点B落在AC边上,记作点B′,连接B′E. 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0). 如图,等腰△ABC中,AB=AC=13cm,BC=10cm,求外接圆的半径.
如图,等腰△ABC中,AB=AC=13cm,BC=10cm,求外接圆的半径.