题目内容
11.已知抛物线y=x2-4x+3.(1)求抛物线的对称轴和顶点坐标.
(2)当x取什么值时,函数y随x的增大而增大.
分析 (1)首先把抛物线y=x2-4x+3转化为顶点坐标式,进而求出抛物线的对称轴和顶点坐标;
(2)由于a=1>0,结合抛物线开口方向进而得到函数y随x的增大而增大时x的取值范围.
解答 解:(1)∵抛物线解析式为y=x2-4x+3,
∴y=(x-2)2-1,
∴抛物线的对称轴为x=2,顶点坐标为(2,-1);
(2)∵a=1>1,
∴抛物线的开口向上,
又∵对称轴为x=2,
∴当x>2时,函数y随x的增大而增大.
点评 本题主要考查了二次函数的性质,解答本题的关键是把抛物线的一般式写成顶点坐标式,此题难度一般.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
19.在下列四组点中,可以在同一个正比例函数图象上的一组点是( )
| A. | (-2,-3),(4,-6) | B. | (-2,3),(4,6) | C. | (2,-3),(-4,6) | D. | (2,3),(-4,6) |
 (1)已知点A(m+1,2n-3)关于原点对称的点A1(2m+1,-n-1),求m、n的值.
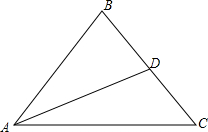
(1)已知点A(m+1,2n-3)关于原点对称的点A1(2m+1,-n-1),求m、n的值. 如图,在△ABC与△ABD中,AD与BC相交于0点,∠1=∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC=BD.并给出证明.
如图,在△ABC与△ABD中,AD与BC相交于0点,∠1=∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC=BD.并给出证明.