题目内容
9．已知一次函数y=（3-k）x-2k2+18．（1）k为何值时，它的图象经过原点？
（2）k为何值时，它的图象经过点（0，-2）且y随x增大而减小？
分析 （1）把原点代入解析式，即可求得k的值；
（2）首先根据图象经过（0，-2）求得k值，然后根据函数图象的增减性确定k的值即可．
解答 解：（1）把（0，0）代入解析式得：-2k2+18=0，
解得：k=±3，又3-k≠0，
所以k=-3；
（2）∵y=（2+k）x-2k2+18的图象经过点（0，-2），
∴-2k2+18=-2，
解得：k=±$\sqrt{10}$，∵y随x的增大而减小，
∴3-k＜0，即k＞3．
∴k=$\sqrt{10}$．
点评 本题考查了一次函数图象上点的坐标特征及函数性质，是基础题型，熟练掌握一次函数的性质是解题的关键．
练习册系列答案
相关题目
9．
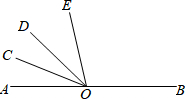如图，已知O为直线AB上一点，OC平分∠AOD，∠BOD=4∠DOE，∠COE=α，则∠BOE的度数为（ ）
如图，已知O为直线AB上一点，OC平分∠AOD，∠BOD=4∠DOE，∠COE=α，则∠BOE的度数为（ ）| A． | 360°-4α | B． | 180°-4α | C． | α | D． | 270°-3α |
如图，在Rt△ABO 中，AO=4，BO=3，动点P从A点出发，以每秒2个单位的速度沿AO方向向点O匀速运动，同时动点Q从B点出发，以每秒1个单位的速度沿BA方向向点A匀速运动，当一个点停止运动，另一个点也随之停止运动，连接PQ，设运动时间为t（s）．
已知抛物线的表达式为y=-x2+6x+c．
如图，已知直线m⊥n，在某平面直角坐标系中，x轴∥直线m，y轴∥直线n，点A、B的坐标分别为（-4，2），（2，-4），点A，O4，B在同一条直线上，则坐标原点为（ ）