题目内容
解方程或不等式：
（1）（3x-1）2-（x-3）（x+3）=8（x+1）2；
（2）（x-2）2-（2x-5）2≥3（1-x2）+8．
（1）（3x-1）2-（x-3）（x+3）=8（x+1）2；
（2）（x-2）2-（2x-5）2≥3（1-x2）+8．
考点：整式的混合运算,解一元一次不等式
专题：计算题
分析：（1）原式两边利用完全平方公式及平方差公式化简，去括号，移项合并，将x系数化为1，即可求出解；
（2）原式两边利用完全平方公式及平方差公式化简，去括号，移项合并，将x系数化为1，即可求出解集．
（2）原式两边利用完全平方公式及平方差公式化简，去括号，移项合并，将x系数化为1，即可求出解集．
解答：解：（1）去括号得：9x2-6x+1-x2+9=8x2+16x+8，
移项合并得：22x=2，
解得：x=
；
（2）去括号得：x2-4x+4-4x2+20x-25≥3-3x2+8，
移项合并得：16x≥32，
解得：x≥2．
移项合并得：22x=2，
解得：x=
| 1 |
| 11 |
（2）去括号得：x2-4x+4-4x2+20x-25≥3-3x2+8，
移项合并得：16x≥32，
解得：x≥2．
点评：此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
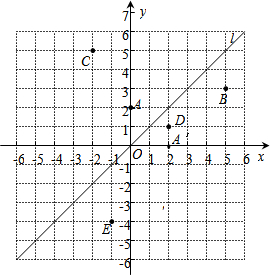如图，在平面直角坐标系中，直线l的解析式是y=x．
