题目内容
4.若O为△ABC的重心,△BOC的面积为4,则△ABC的面积为12.分析 分别延长AO、BO、CO,交BC、AC、AB于点D、E、F,根据三角形重心的定义得到AD、BE、CF是△ABC的中线,根据三角形的中线把三角形分为面积相等的两个三角形进行解答.
解答 解: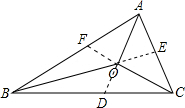 如图,分别延长AO、BO、CO,交BC、AC、AB于点D、E、F,
如图,分别延长AO、BO、CO,交BC、AC、AB于点D、E、F,
∵O是△ABC的重心,
∴AD、BE、CF是△ABC的中线,
∴S△ABD=S△ABE=$\frac{1}{2}$S△ABC,S△BOD=S△AOE,
又∵S△AOE=S△COE,S△BOD=S△COD,
∴S△AOC=S△BOC,
同理可得S△BOC=S△AOB,
∴S△AOB=S△BOC=S△AOC,
∴△ABC的面积为:4×3=12.
故答案为:12.
点评 本题考查了三角形的重心,掌握三角形的重心是三角形三边中线的交点是解题的关键.

练习册系列答案
相关题目
9.在下列函数中表示关于x的反比例函数的是( )
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=$\frac{2}{x+1}$ | D. | y=$\frac{2}{{x}^{2}}$ |
16.不等式组$\left\{\begin{array}{l}{x-1≤0}\\{6-3x>0}\end{array}\right.$的解集为( )
| A. | x≤1 | B. | x>-2 | C. | -2≤x≤1 | D. | 无解 |
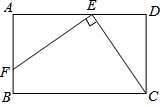 如图,在矩形ABCD中,EF⊥CE,EF=CE,DE=2cm,矩形的周长为32cm,求矩形ABCD的面积.
如图,在矩形ABCD中,EF⊥CE,EF=CE,DE=2cm,矩形的周长为32cm,求矩形ABCD的面积.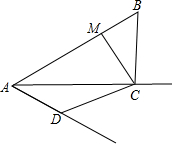 如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.
如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.
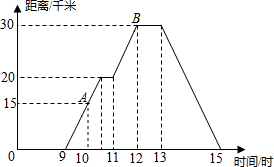 小明家在下白石,他很想一个人去穆阳白云山玩,不过他要先到赛岐停留下,然后在接着去穆阳白云山,他把一天的时间做了一个规划,下面是小明一天从0点到15点的离家距离的情况.
小明家在下白石,他很想一个人去穆阳白云山玩,不过他要先到赛岐停留下,然后在接着去穆阳白云山,他把一天的时间做了一个规划,下面是小明一天从0点到15点的离家距离的情况.