题目内容
5.如图,下列图形中,每个正方形网格都是由边长为1的小正方形组成,则图中阴影部分面积最大的是( )| A. |  | B. |  | C. |  | D. |  |
分析 运用三角形的面积公式分别求出每个选项中,阴影部分的面积,经比较即可解决问题.
解答 解:对于选项A,
图中阴影部分面积
=${3}^{2}-\frac{1}{2}×2×2-\frac{1}{2}×2×1-\frac{1}{2}×3×2$
=9-2-1-3=3;
对于选项B,
图中阴影部分面积
=${3}^{2}-4×\frac{1}{2}(1+2)×1$
=9-6=3;
对于选项C,
图中阴影部分面积
=${3}^{2}-2×\frac{1}{2}(1+3)×1-2×\frac{1}{2}×2×1$
=9-4-2=3;
对于选项D,
图中阴影部分面积
=${3}^{2}-\frac{1}{2}×2×1×2-\frac{1}{2}×2×2-\frac{1}{2}×3×1$
=9-2-2-1.5
=3.5,
∴图中阴影部分面积最大的是选项D中的阴影部分的面积,
故选D.
点评 该题以正方形为载体,主要考查了正方形的面积公式、三角形的面积公式及其应用问题;解题的关键是灵活运用三角形的面积公式来分析、判断、推理或解答.

练习册系列答案
相关题目
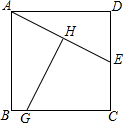 如图,E是正方形ABCD的边CD的中点,AE的垂直平分线分别交AE、BC于H、G,若CG=7,则正方形ABCD的面积等于64.
如图,E是正方形ABCD的边CD的中点,AE的垂直平分线分别交AE、BC于H、G,若CG=7,则正方形ABCD的面积等于64.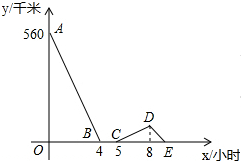 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为60千米.
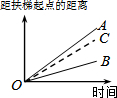
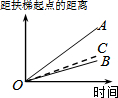
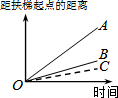
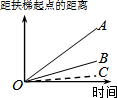
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为60千米.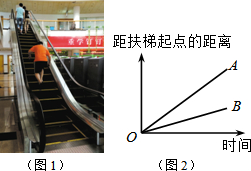 大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )
大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )