题目内容
10.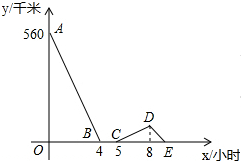 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为60千米.
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为60千米.
分析 先根据题意得出慢车往返分别用了4小时,慢车行驶4小时的距离,快车3小时即可行驶完,进而求出快车速度以及利用两车速度之比得出慢车速度;再求出快车到达甲地用时,即可求出快车到达甲地时慢车据甲地的距离.
解答 解:由题意可得出:慢车和快车经过4个小时后相遇,相遇后停留了1个小时,出发后两车之间的距离开始增大,快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,
∴设慢车速度为3xkm/h,快车速度为4xkm/h,
∴(3x+4x)×4=560,x=20,
∴快车的速度是80km/h,慢车的速度是60km/h.
快车和慢车相遇地离甲地的距离为4×60=240km,
当慢车行驶了7小时后,快车已到达甲地,此时两车之间的距离为240-3×60=60km.
故答案为60.
点评 本题主要考查的是函数图象的应用,根据图象得出相应的信息是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
18. 下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
(1)李刚6次成绩的极差是10分;中位数是90分.
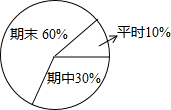
(2)如果用如图的权重给李刚打分,他应该得多少分?
 下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
下表是李刚一学期数学成绩记录,根据信息回答下面的问题:| 考试类别 | 平时 | 期中考试 | 期末考试 | |||
| 第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
| 成绩 | 88 | 86 | 90 | 92 | 90 | 96 |
(2)如果用如图的权重给李刚打分,他应该得多少分?
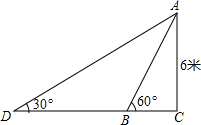 如图,某水上乐园有一个滑梯AB,高度AC为6米,倾斜角为60°,暑期将至,为改善滑梯AB的安全性能,把倾斜角由60°减至30°
如图,某水上乐园有一个滑梯AB,高度AC为6米,倾斜角为60°,暑期将至,为改善滑梯AB的安全性能,把倾斜角由60°减至30°