题目内容
20.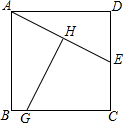 如图,E是正方形ABCD的边CD的中点,AE的垂直平分线分别交AE、BC于H、G,若CG=7,则正方形ABCD的面积等于64.
如图,E是正方形ABCD的边CD的中点,AE的垂直平分线分别交AE、BC于H、G,若CG=7,则正方形ABCD的面积等于64.
分析 连接AG、EG,设CE=x,则AB=BC=2x,BG=2x-7,根据线段垂直平分线的性质得出AG=EG,根据勾股定理得出方程,解方程即可求出边长,即可得出面积.
解答 解:连接AG、EG,如图所示: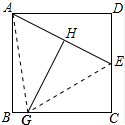 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=CD,
∵E是正方形ABCD的边CD的中点,
∴CE=$\frac{1}{2}$CD,
设CE=x,则AB=BC=2x,BG=2x-7,
∵AE的垂直平分线分别交AE、BC于H、G,
∴AG=EG,
在Rt△AGH和Rt△EGH中,
根据勾股定理得:AG2=AB2+BG2,EG2=CE2+CG2,
∴(2x)2+(2x-7)2=x2+72,
解得:x=4,
∴AB=8,
∴正方形ABCD的面积=AB2=82=64.
故答案为:64.
点评 本题考查了正方形的性质、线段垂直平分线的性质以及勾股定理的运用;根据勾股定理列出方程是解决问题的关键.

练习册系列答案
相关题目
8.甲、乙两个同学在四次模拟试中,数学的平均成绩都是112分,方差分别是S甲2=5,S乙2=12,则成绩比较稳定的是( )
| A. | 甲 | B. | 乙 | C. | 甲和乙一样 | D. | 无法确定 |
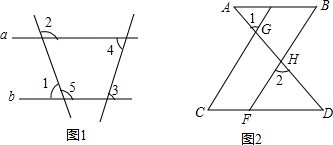 看图填空:
看图填空:
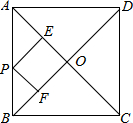 如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5.
如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5.



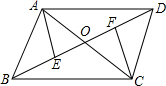 如图,BD是?ABCD的对角线,E、F分别为BD上两点,AC交BD于O.
如图,BD是?ABCD的对角线,E、F分别为BD上两点,AC交BD于O.