题目内容
2.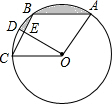 如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 4π-12$\sqrt{3}$ | B. | 4π-6$\sqrt{3}$ | C. | 4π | D. | 6π |
分析 根据菱形的性质得出∠AOC=120°,AB=BC,进一步求得∠AOB=∠BOC=$\frac{1}{2}$∠AOC=60°,∠BOD=∠COD=$\frac{1}{2}$∠BOC=30°,解直角三角形OBE求得半径,然后根据S阴影=S扇形AOB+S扇形BOC-S扇形DOC-S△AOB-S△BOE即可求得.
解答 解:∵四边形ABCO是菱形,∠ABC=120°,
∴∠AOC=120°,AB=BC,
∴$\widehat{AB}$=$\widehat{BC}$,
∴∠AOB=∠BOC=$\frac{1}{2}$∠AOC=60°,
∵OB=OC,OD⊥CB,
∴∠BOD=∠COD=$\frac{1}{2}$∠BOC=30°,
∵OE=2$\sqrt{3}$,
∴OB=$\frac{OE}{cos30°}$=4,
∴AB=BC=4,
∵S扇形AOB=S扇形BOC=$\frac{60π×{4}^{2}}{360}$=$\frac{8}{3}$π,S扇形DOC=$\frac{1}{2}$=S扇形BOC=$\frac{4}{3}$π,
∴S阴影=S扇形AOB+S扇形BOC-S扇形DOC-S△AOB-S△BOE
=2×$\frac{8}{3}$π-$\frac{4}{3}$π-$\frac{1}{2}$×4×2$\sqrt{3}$-$\frac{1}{2}$×2×2$\sqrt{3}$
=4π-6$\sqrt{3}$,
故选B.
点评 此题考查了扇形的面积公式,掌握扇形面积计算公式的计算方法是解决问题的关键.

练习册系列答案
相关题目
7.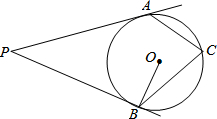 如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
 如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )| A. | 50° | B. | 60° | C. | 65° | D. | 70° |
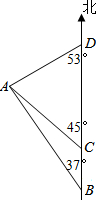 如图,一艘货船从港口B出发,沿正北方向航行至港口D,在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处时,测得A处在C处的西北方向上,航行至D处时,测得A处在C处的南偏西53°方向上,已知A,B之间的距离是100海里,
如图,一艘货船从港口B出发,沿正北方向航行至港口D,在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处时,测得A处在C处的西北方向上,航行至D处时,测得A处在C处的南偏西53°方向上,已知A,B之间的距离是100海里,