题目内容
15.正十二边形的每个内角为150度,中心角为30度.分析 首先求得每个外角的度数,然后根据外角与相邻的内角互为邻补角得出每个内角的度数,由正多边形的中心角定义即可得出结果.
解答 解:正十二边形的每个外角的度数是:$\frac{360°}{12}$=30°,
则每一个内角的度数是:180°-30°=150°;
正十二边形的中心角为$\frac{360°}{12}$=30°.
故答案为:150,30.
点评 本题考查了正多边形的性质、中心角的定义;掌握多边形的外角和等于360度,正确理解内角与外角的关系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.一个正方形有一个外接圆和一个内切圆,这两个圆的面积比是( )
| A. | 3:2 | B. | 2:1 | C. | 4:9 | D. | 9:25 |
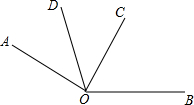 如下图,∠AOC是直角,OD平分∠AOC,∠BOC=60° 求:
如下图,∠AOC是直角,OD平分∠AOC,∠BOC=60° 求: