题目内容
11.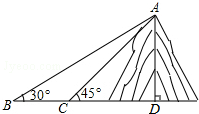 如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD是多少?(结果保留整数,测角仪忽略不计,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.73)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD是多少?(结果保留整数,测角仪忽略不计,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.73)
分析 设AD=xm,在Rt△ACD中,根据正切的概念用x表示出CD,在Rt△ABD中,根据正切的概念列出方程求出x的值即可.
解答 解:由题意得,∠ABD=30°,∠ACD=45°,BC=100m,
设AD=xm,
在Rt△ACD中,∵tan∠ACD=$\frac{AD}{CD}$,
∴CD=AD=x,
∴BD=BC+CD=x+100,
在Rt△ABD中,∵tan∠ABD=$\frac{AD}{BD}$,
∴x=$\frac{\sqrt{3}}{3}$(x+100),
∴x=50($\sqrt{3}$+1)≈137米,
答:山高AD约为137米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.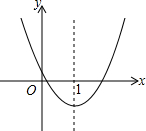 如图,二次函数y=ax2+bx+c的图象如图所示,则下列说法①ac<0;②2a+b<0;③当x=1时,a+b+c>0;④当x=-1时,a-b+c>0;⑤关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.你认为其中正确的有( )
如图,二次函数y=ax2+bx+c的图象如图所示,则下列说法①ac<0;②2a+b<0;③当x=1时,a+b+c>0;④当x=-1时,a-b+c>0;⑤关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.你认为其中正确的有( )
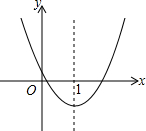 如图,二次函数y=ax2+bx+c的图象如图所示,则下列说法①ac<0;②2a+b<0;③当x=1时,a+b+c>0;④当x=-1时,a-b+c>0;⑤关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.你认为其中正确的有( )
如图,二次函数y=ax2+bx+c的图象如图所示,则下列说法①ac<0;②2a+b<0;③当x=1时,a+b+c>0;④当x=-1时,a-b+c>0;⑤关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.你认为其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.化简$\frac{m-1}{m}$÷$\frac{{m}^{2}-1}{{m}^{2}}$的结果是( )
| A. | $\frac{m}{m+1}$ | B. | $\frac{1}{m-1}$ | C. | $\frac{m}{m-1}$ | D. | m |
3.计算(a-3)2的结果是( )
| A. | a2-9 | B. | a2+9 | C. | a2-6a+9 | D. | a2+6a+9 |
 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.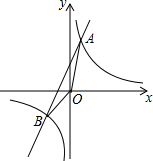 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).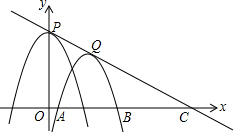 如图,点P是抛物线y=-x2+4的顶点,将抛物线平移,平移后的抛物线与x轴交于A,B两点(A在B的左侧)顶点Q落在第一象限内,且△ABQ是等边三角形,直线PQ与x轴交于点C,若PQ=$\sqrt{3}$,则BC=3$\sqrt{2}$-$\sqrt{3}$.
如图,点P是抛物线y=-x2+4的顶点,将抛物线平移,平移后的抛物线与x轴交于A,B两点(A在B的左侧)顶点Q落在第一象限内,且△ABQ是等边三角形,直线PQ与x轴交于点C,若PQ=$\sqrt{3}$,则BC=3$\sqrt{2}$-$\sqrt{3}$.