题目内容

1．如图，点D、E、F分别是△ABC各边中点．求证：四边形ADEF是平行四边形．

分析 根据三角形的中位线定理可得DE∥AC，EF∥AB，再根据两组对边分别平行的四边形是平行四边形证明即可．

解答 证明：∵D、E分别为AB、BC的中点，
∴DE∥AC，
∵E、F分别为BC、AC中点，
∴EF∥AB，
∴四边形ADEF是平行四边形．

点评 此题主要考查了三角形的中位线定理，勾股定理以及平行四边形的判定定理，关键是掌握三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．

练习册系列答案
相关题目
20．如图，正方形ABCD中，E为CD的中点，F是DA的中点，连接BE，与CF相交于P，求证：AP=AB．
12．已知一个多边形，除了一个内角外，其余各内角和是2400度，求这个内角的度数．
9．已知a=$\sqrt{2}$-1，b=$\sqrt{2}$+1，分别求下列各式的值．
（1）a2+b2；
（2）$\frac{b}{a}$-$\frac{a}{b}$．
16．如图，已知AB∥CD，BE平分∠ABF，DF平分∠CDE，若∠E=70°，∠F=65°，则∠BGD=90°．
6．如图，在下列条件中，一定能得到AB∥CD是（　　）
A．∠1=∠2B．∠3=∠4C．∠5=∠6D．∠7=∠8
13．下列等式一定成立的是（　　）
A．$\frac{n}{m}$=$\frac{{n}^{2}}{{m}^{2}}$B．$\frac{n}{m}$=$\frac{n-1}{m-1}$C．$\frac{n}{m}$=$\frac{n+1}{m+1}$D．$\frac{n}{m}$=$\frac{na}{ma}$（a≠0）
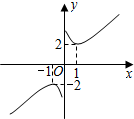10．已知函数y=x+x-1，其图象如图．给出下列几个命题：①该函数的图象是中心对称图形；②y的值不可能为1；③当x＜0时，该函数在x=-1时取得最大值-2；④在每个象限内，函数值y随自变量x的增大而增大．其中正确的个数是（　　）
A．0B．1C．2D．3
11．南海是我们固有领土，南海资源丰富，其面积约为350万平方千米，相当于我国的渤海、黄海和东海总面积的3倍，其中350万用科学记数法表示为（　　）
A．3.5×106B．3.5×107C．0.35×108D．3.5×109

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网