题目内容
1.化简下列各式:(1)4(a+b)2-2(a+b)(2a-2b)
(2)$-(m+2)÷(m-1+\frac{2m+1}{m+1})-\frac{1}{m}$.
分析 (1)先根据完全平方公式和多项式乘以多项式的法则计算,再合并同类项即可;
(2)根据分式混合运算的顺序,先算括号里,再乘除,最后加减,即可解答.
解答 解:(1)原式=4(a2+2ab+b2)-4(a2-b2)=4a2+8ab+4b2-4a2+4b2=8ab+8b2;
(2)原式=$-(m+2)÷(\frac{{{m^2}-1+2m+1}}{m+1})-\frac{1}{m}$=$-(m+2)•\frac{m+1}{m(m+2)}-\frac{1}{m}$=$-\frac{m+1}{m}-\frac{1}{m}$=$-\frac{m+2}{m}$.
点评 本题主要考查整式的混合运算及分式的混合运算,熟记各运算法则是解决此题的关键.

练习册系列答案
相关题目
13.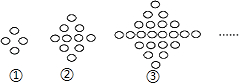 如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
 如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )| A. | 190 | B. | 94 | C. | 70 | D. | 46 |
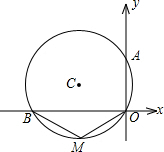 如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°.
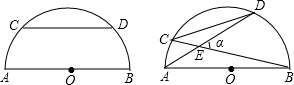
如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°.  如图,直线AB、CD相交于点O,若∠AOD=28°,则∠BOC=28°,∠AOC=152°.
如图,直线AB、CD相交于点O,若∠AOD=28°,则∠BOC=28°,∠AOC=152°. 如图,在△ABC中,点I是外心,∠BIC=110°,则∠A=55°.
如图,在△ABC中,点I是外心,∠BIC=110°,则∠A=55°.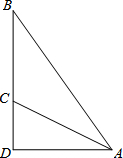 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.