题目内容
11.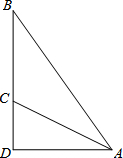 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.
分析 设CD=x,则AD=2x,根据勾股定理求出AC的长,从而求出CD、AC的长,然后根据勾股定理求出BD的长,即可求出BC的长.
解答 解:设CD=x,则AD=2x,
由勾股定理可得,AC=$\sqrt{{x}^{2}+(2x)^{2}}$=$\sqrt{5}$x,
∵AC=3$\sqrt{5}$米,
∴$\sqrt{5}$x=3$\sqrt{5}$,
∴x=3(米),
∴CD=3米,
∴AD=2×3=6米,
在Rt△ABD中,BD=$\sqrt{1{0}^{2}-{6}^{2}}$=8(米),
∴BC=8-3=5(米).
故答案为:5米.
点评 本题考查了解直角三角形的应用--坡度坡角问题,找到合适的直角三角形,熟练运用勾股定理是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
2.计算($\frac{1}{2}$)2014•22014的结果是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 24028 |
19. 如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )
如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )
 如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )
如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )| A. | 40° | B. | 35° | C. | 25° | D. | 20° |
6.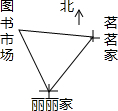 周末茗茗、丽丽两人相约去图书市场,8时丽丽开始从家以2千米/小时的速度沿北偏西25°的方向步行,9时茗茗开始从自己家以4千米/小时的速度沿一定的方向骑行,10时她们同时到达图书市场,如图所示,已知茗茗、丽丽两家相距4千米,则茗茗家与丽丽家的相对位置是( )
周末茗茗、丽丽两人相约去图书市场,8时丽丽开始从家以2千米/小时的速度沿北偏西25°的方向步行,9时茗茗开始从自己家以4千米/小时的速度沿一定的方向骑行,10时她们同时到达图书市场,如图所示,已知茗茗、丽丽两家相距4千米,则茗茗家与丽丽家的相对位置是( )
 周末茗茗、丽丽两人相约去图书市场,8时丽丽开始从家以2千米/小时的速度沿北偏西25°的方向步行,9时茗茗开始从自己家以4千米/小时的速度沿一定的方向骑行,10时她们同时到达图书市场,如图所示,已知茗茗、丽丽两家相距4千米,则茗茗家与丽丽家的相对位置是( )
周末茗茗、丽丽两人相约去图书市场,8时丽丽开始从家以2千米/小时的速度沿北偏西25°的方向步行,9时茗茗开始从自己家以4千米/小时的速度沿一定的方向骑行,10时她们同时到达图书市场,如图所示,已知茗茗、丽丽两家相距4千米,则茗茗家与丽丽家的相对位置是( )| A. | 茗茗家在丽丽家北偏西55°方向 | B. | 茗茗家在丽丽家北偏东55°方向 | ||
| C. | 茗茗家在丽丽家南偏西35°方向 | D. | 茗茗家在丽丽家北偏东35°方向 |
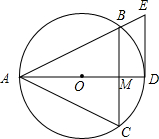 已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.
已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.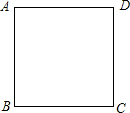 在数学课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D,第二次逆时针方向跳2步到达顶点B,第三次顺时针方向跳3步到达顶点C,第四次逆时针方向跳4步到达顶点C,…,以此类推,跳动第2014次到达的顶点是( )
在数学课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D,第二次逆时针方向跳2步到达顶点B,第三次顺时针方向跳3步到达顶点C,第四次逆时针方向跳4步到达顶点C,…,以此类推,跳动第2014次到达的顶点是( )