Question

13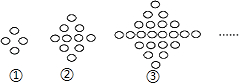．如图，第①个图形中有4个“○”，第②个图形中有10个“○”，第③个图形中有22个“○”，…，那么第⑤个图形中“○”的个数是（　　）

• A． 190
• B． 94
• C． 70
• D． 46

Answer 1

分析 由图可知：第①个图形中有1+2+1=4个“○”，第②个图形中有1+2+4+2+1=10个“○”，第③个图形中有1+2+4+8+4+2+1=22个“○”，…，得出第n个图形中有1+2+2²+2³+…+2ⁿ…+2³+2²+2+1个“○”，由此规律求得答案即可．

解答 解：∵第①个图形中有1+2+1=4个“○”，
第②个图形中有1+2+4+2+1=10个“○”，
第③个图形中有1+2+4+8+4+2+1=22个“○”，
…，
∴第⑤个图形中“○”的个数是1+2+4+8+16+32+16+8+4+2+1=94．
故选：B．

点评 此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．