题目内容
13. 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S9的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S9的值为( )| A. | ($\frac{1}{2}$)6 | B. | ($\frac{1}{2}$)7 | C. | ($\frac{\sqrt{2}}{2}$)6 | D. | ($\frac{\sqrt{2}}{2}$)7 |
分析 根据等腰直角三角形的性质可得出S2+S2=S1,写出部分Sn的值,根据数的变化找出变化规律“Sn=($\frac{1}{2}$)n-3”,依此规律即可得出结论.
解答 解:在图中标上字母E,如图所示.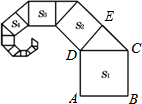
∵正方形ABCD的边长为2,△CDE为等腰直角三角形,
∴DE2+CE2=CD2,DE=CE,
∴S2+S2=S1.
观察,发现规律:S1=22=4,S2=$\frac{1}{2}$S1=2,S3=$\frac{1}{2}$S2=1,S4=$\frac{1}{2}$S3=$\frac{1}{2}$,…,
∴Sn=($\frac{1}{2}$)n-3.
当n=9时,S9=($\frac{1}{2}$)9-3=($\frac{1}{2}$)6,
故选:A.
点评 本题考查了等腰直角三角形的性质、勾股定理以及规律型中数的变化规律,解题的关键是找出规律“Sn=($\frac{1}{2}$)n-3”.本题属于中档题,难度不大,解决该题型题目时,写出部分Sn的值,根据数值的变化找出变化规律是关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
3.下列图形,既是轴对称图形又是中心对称图形的是( )
| A. | 平行四边形 | B. | 正五边形 | C. | 等边三角形 | D. | 矩形 |
1.已知2m=3,4n=5,则23m+2n的值为( )
| A. | 45 | B. | 135 | C. | 225 | D. | 675 |
8.加工一零件,要求直径为10mm,现由甲、乙两个车间工人加工,加工的零件各取5件,测得的结果是:
甲:10.05,10.02,9.97,9.96,10.00;
乙:10.00,10.01,10.02,9.97,10.00.
这两个车间工人中生产质量比较稳定的是( )
甲:10.05,10.02,9.97,9.96,10.00;
乙:10.00,10.01,10.02,9.97,10.00.
这两个车间工人中生产质量比较稳定的是( )
| A. | 甲 | B. | 乙 | C. | 无法判断 | D. | 以上都不对 |
5.已知四个实数:3,$-\sqrt{2}$,π,$\sqrt{5}$,其中最大的实数是( )
| A. | 3 | B. | $-\sqrt{2}$ | C. | π | D. | $\sqrt{5}$ |
14.下列图案中,只要用其中一部分平移一次就可以得到的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,六个正方形内分别标有“0,1,2,5,数,学“,这六个正方形经过折叠后能形成一个正方体,那么,其中与“5”相对的是( )
如图,六个正方形内分别标有“0,1,2,5,数,学“,这六个正方形经过折叠后能形成一个正方体,那么,其中与“5”相对的是( ) 如图,点A、C为反比例函数y=$\frac{k}{x}(x<0)$图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为$\frac{3}{2}$时,k的值为( )
如图,点A、C为反比例函数y=$\frac{k}{x}(x<0)$图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为$\frac{3}{2}$时,k的值为( )