题目内容
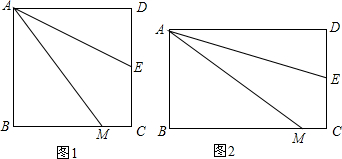
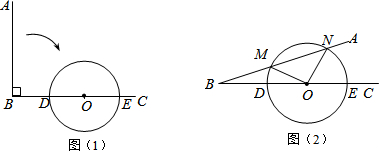
15.如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.(1)求证:AD+MC=DE+BM;
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由.
(3)图1中,若正方形的边长是2,求四边形AMCE的面积.
分析 (1)从平行线和中点这两个条件出发,延长AE、BC交于点N,易证△ADE≌△NCE,从而有AD=CN,证明AM=NM即可得出AM=AD+MC;作FA⊥AE交CB的延长线于点F,易证AM=FM,需要证明FB=DE;要证FB=DE,只需证明它们所在的两个三角形全等,即可得出AM=FB+BM=DE+BM,即可得出结论;
(2)仿照(1)中的证明思路即可证到AM=AD+MC仍然成立;采用反证法,并仿照(1)中的证明思路即可证到AM=DE+BM不成立;
(3)由(1)得出DE=2MC,得出MC=$\frac{1}{2}$,BM=$\frac{3}{2}$,四边形AMCE的面积=正方形ABCD的面积-△ABM的面积-△ADE的面积,即可得出结果.
解答 (1)证明:延长AE、BC交于点N,过点A作AF⊥AE,交CB的延长线于点F,如图1所示,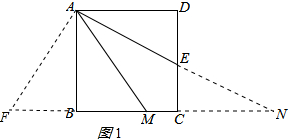
∵四边形ABCD是正方形,
∴AD∥BC.
∴∠DAE=∠ENC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠ENC=∠MAE.
∴AM=MN.
在△ADE和△NCE中,
$\left\{\begin{array}{l}{∠DAE=∠CNE}&{\;}\\{∠AED=∠NEC}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△ADE≌△NCE(AAS).
∴AD=NC.
∴AM=MN=NC+MC=AD+MC.
∵四边形ABCD是正方形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.
∵AF⊥AE,
∴∠FAE=90°.
∴∠FAB=90°-∠BAE=∠DAE.
在△ABF和△ADE中,
$\left\{\begin{array}{l}{∠FAB=∠EAD}&{\;}\\{AB=AD}&{\;}\\{∠ABF=∠D=90°}&{\;}\end{array}\right.$,
∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
∴AD+MC=DE+BM.
(2)解:AD+MC=DE+BM不成立;理由如下:
延长AE、BC交于点P,过点A作AQ⊥AE,交CB的延长线于点Q,如图2所示,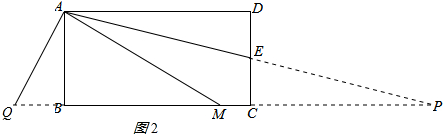
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DAE=∠EPC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠EPC=∠MAE.
∴MA=MP.
在△ADE和△PCE中,
$\left\{\begin{array}{l}{∠DAE=∠CPE}&{\;}\\{∠AED=∠PEC}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△ADE≌△PCE(AAS).
∴AD=PC.
∴AM=MP=PC+MC=AD+MC.
假设AM=DE+BM成立.
∵四边形ABCD是矩形,
∴∠BAD=∠D=∠ABC=90°,AB∥DC.
∵AQ⊥AE,
∴∠QAE=90°.
∴∠QAB=90°-∠BAE=∠DAE.
∴∠Q=90°-∠QAB=90°-∠DAE=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠QAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠QAB=∠QAM.
∴∠Q=∠QAM.
∴AM=QM.
∴AM=QB+BM.
∵AM=DE+BM,
∴QB=DE.
在△ABQ和△ADE中,
$\left\{\begin{array}{l}{∠QAB=∠EAD}&{\;}\\{∠ABQ=∠D=90°}&{\;}\\{BQ=DE}&{\;}\end{array}\right.$,
∴△ABQ≌△ADE(AAS).
∴AB=AD.
与条件“AB≠AD“矛盾,故假设不成立.
∴AM=DE+BM不成立.
∴AD+MC=DE+BM不成立.
(3)解:∵AD+MC=DE+BM,
∴AD+MC=DE+BC-MC,
∴DE=2MC,
∵正方形ABCD的边长为2,
∴AB=BC=CD=AD=2,DE=1,
∴MC=$\frac{1}{2}$,
∴BM=2-$\frac{1}{2}$=$\frac{3}{2}$,
∴四边形AMCE的面积=正方形ABCD的面积-△ABM的面积-△ADE的面积=2×2-$\frac{1}{2}$×2×$\frac{3}{2}$-$\frac{1}{2}$×2×1=$\frac{3}{2}$.
点评 本题考查了正方形及矩形的性质、全等三角形的性质和判定、等腰三角形的判定、平行线的性质、角平分线的定义等知识,考查了基本模型的构造(平行加中点构造全等三角形),考查了反证法的应用,综合性比较强.添加辅助线,构造全等三角形是解决问题的关键.

| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 三角形的中位线平行于第三边且等于第三边的一半 | |
| D. | 三角形的一条中线能将三角形分成面积相等的两部分 |
| A. | (-a)(-a)2=-a3 | B. | -2x2(-3x)=-6x4 | C. | (-a)3(-a)2=-a5 | D. | (-a)3(-a)3=a6 |
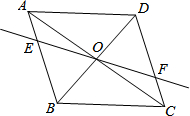 如图,在?ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.
如图,在?ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.
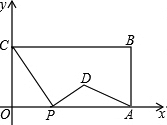 如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=6,OC=4.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则
如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=6,OC=4.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则